УРОК № 9
Тема. Решение упражнений
Цель урока: формирование умений учащихся применять теоремы синусов и косинусов и следствий из них к решению задач.
Тип урока: комбинированный.
Наглядность и оборудование: таблица «Соотношение между сторонами и углами треугольника»[13].
Требования к уровню подготовки учащихся: применяют теорему синусов к решению задач.
Ход урока
И. Проверка домашнего задания
Фронтальное опрос
- 1) Сформулируйте теорему о соотношении между углами треугольника и противолежащими сторонами.
- 2) Сформулируйте обратную теорему (теорему о соотношении между сторонами треугольника и противолежащими углами).
- 3) Устная проверка задачи № 1 за вопросами.
а) Какие стороны лежат против углов А, В, С?
б) Какая из сторон треугольника является наибольшей? Почему?
в) Какая из сторон треугольника является наименьшей? Почему?
г) может Ли данный треугольник быть равнобедренным? Почему?
Устная проверка задачи № 2 за вопросами
а) Какие углы лежат в треугольнике ABC против сторон АВ, ВС, АС соответственно?
б) Какой из углов треугольника является наибольшим? Почему?
в) Какой из углов треугольника является наименьшим? Почему?
Проверка решения задачи № 3
(по записям на доске, сделанными до начала урока)
Один из углов (рис. 35), ADC или CDB, неострый. (?)
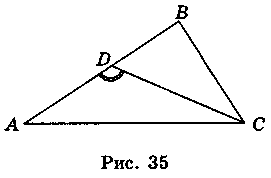
Пусть для определенности  ADС ≥ 90°, тогда
ADС ≥ 90°, тогда  A 90°. (?)
A 90°. (?)
Из треугольника ADC имеем: DC AC (?)
Следовательно, отрезок CD меньше хотя бы за одну из сторон - АС или ВС.
[Знак (?) означает, что ученики должны объяснить: почему это так (сделать ссылку на соответствующие определения, теоремы и т.п.).]
II. Закрепление и осмысление изученного материала
Решение задач
- 1) Определите вид треугольника (относительно углов), если его стороны равны 11 см, 17 см, 21 cm.
Решение
Пусть а = 11 см, b = 17 см, с = 21 см. Наибольшим углом будет угол С, так как он лежит против большей стороны. Тогда с2 = 212 = 441, а2 + b2 = 112 + 172 = 121 + 289 = 410. Поскольку с2 > а2 + b2, то треугольник тупоугольный.
Ответ. Тупоугольный.
- 2) Определите вид треугольника (относительно углов), у которого стороны относятся как: а) 4 : 2 : 3; б) 4 : 5 : 3; в) 3 : 3 : 4.
Ответ, а) Тупоугольный; б) прямоугольный; в) остроугольный.
Коллективное решение задачи
- 1) Найдите радиус круга, описанного вокруг треугольника со сторонами 5 м, 6 м, 7 м.
Решение
Пусть а = 5 м, b = 6 м, с = 7 м, тогда по теореме косинусов имеем:
с2 = a2 + b2 - 2ab c.o.s.c.; 49 = 25 + 36 - 2 ∙ 5 ∙ 6 ∙ c.o.s.c. ; 49 = 61 - 60cosC; 60cosC = 12; c.o.s.c. = 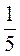 .
.
По основным тождеством cos2C + sin2C = 1 имеем:
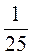 + sin2C = 1; sin2C = 1 -
+ sin2C = 1; sin2C = 1 - 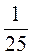 =
= 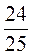 , отсюда sinC =
, отсюда sinC = 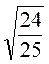 =
= 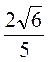 .
.
Тогда по теореме синусов имеем: 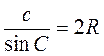 ;
; 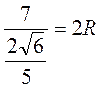 ; R =
; R = 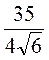 м.
м.
Ответ. 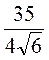 м.
м.
III. Самостоятельная работа
Вариант 1
- 1. Найдите радиус круга, описанного вокруг треугольника, в котором сторона равна 2
 см и лежит против угла 120°. (4 балла)
см и лежит против угла 120°. (4 балла)
- 2. В треугольнике ABC известно, что ВС = 2
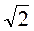 см,
см,  A = 45°,
A = 45°,  C = 30°. Найдите сторону АВ. (4 балла)
C = 30°. Найдите сторону АВ. (4 балла)
- 3. В треугольнике ABC углы А, В, С относятся как 4 : 2 : 3, ВС = 4 см. Найдите сторону АВ. (4 балла)
Вариант 2
- 1. Найдите радиус круга, описанного вокруг треугольника, в котором сторона равна 2
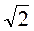 см и лежит против угла 135°. (4 балла)
см и лежит против угла 135°. (4 балла)
- 2. В треугольнике ABC известно, что АВ =
 см, ВС =
см, ВС = 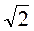 см,
см,  C = 120°. Найдите угол А. (4 балла)
C = 120°. Найдите угол А. (4 балла)
- 3. В треугольнике ABC углы А, В, С относятся как 4 : 2 : 3, ВС = 4 см. Найдите сторону АС. (4 балла)
Ответы к заданиям самостоятельной работы
Вариант 1. 1. 2 см. 2. 2 см. 3. 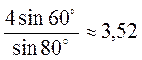 (см).
(см).
Вариант 2. 1. 2 см. 2. 45°. 3. 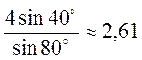 (см).
(см).
IV. Домашнее задание
Решить задачу.
Даны три стороны треугольника: а = 1, b = 2, с = 8. Найдите его углы.
V. Подведение итогов урока
Вопрос к классу
- 1. а : b : с = 2 : 3 : 4. Как относятся синусы углов треугольника?
- 2. Синусы углов треугольника относятся как 3 : 4 : 5. Как относятся стороны треугольника? Определите вид треугольника (по углам).