УРОК 9

Тема. Построение графиков тригонометрических функций

Цель урока: построение графиков функций у = sin х, у = cos x, у = tg х, у = ctg x.

Формирование умений строить графики функций: у = Asin (kx + b), у = Acos (kx + b), у = Atg (kx + b), у = Actg (kx + b).

И. Проверка домашнего задания

1. Один ученик воспроизводит решение упражнения № 24 (1-3).

2. Фронтальная беседа:

1) Назовите явления в природе, которые периодически повторяются.

2) Дайте определение периодической функции.

3) Если функция у = f(x) имеет периодом число Т, то будет периодом этой функции число 2Т, 3T...? Ответ обоснуйте.

4) Найдите наименьший положительный период функций:

a) y = cos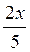; б) y = sin 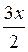; в) у = tg 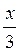; г) у = .

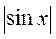5) периодическая функция у = С? Если да, то укажите период этой функции.

II. Построение графика функции у = sin х

Для построения графика функции у = sin x воспользуемся единичным кругом. Построим единичный круг радиусом 1 см (2 клетки). Справа построим систему координат, как на рис. 57.

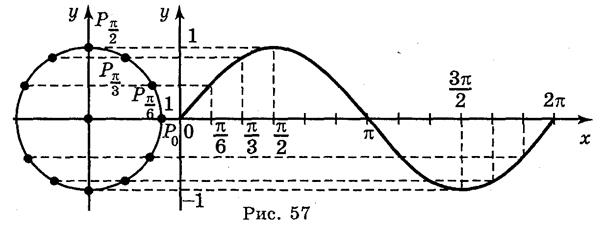
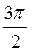На ось ОХ нанесем точки ; π; ; 2π (соответственно 3 ячейки, 6 ячеек 9 ячеек, 12 ячеек). Разделим первую четверть единичного круга на три равные части и на столько же частей отрезок 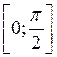оси абсцисс. Перенесем значение синуса до соответствующих точек оси ОХ. Получим точки, которые надо соединить плавной линией. Затем разделим вторую, третью и четвертую четверть единичного круга также на три равные части и перенесем значение синуса до соответствующей точки оси ОХ. Последовательно соединив все полученные точки, получим график функции у = sin х на промежутке [0;π].

За то что функция у = sin x периодическая с периодом 2π, то для построения графика функции у = sin x на всей прямой ОХ достаточно параллельно перенести построен график вдоль оси ОХ на 2π, 4π, 6π... единиц влево и вправо (рис. 58).

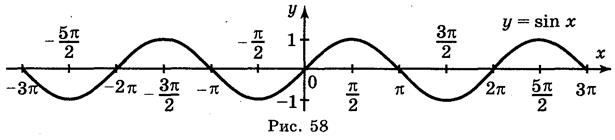
Кривая, которая является графиком функции у = sin x, называют синусоидой.

Выполнение упражнений______________________________

1. Постройте графики функций.

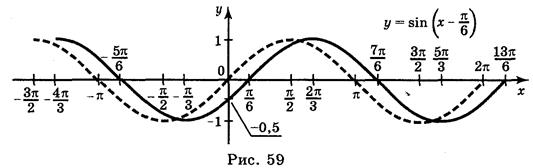
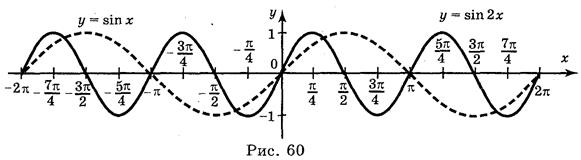
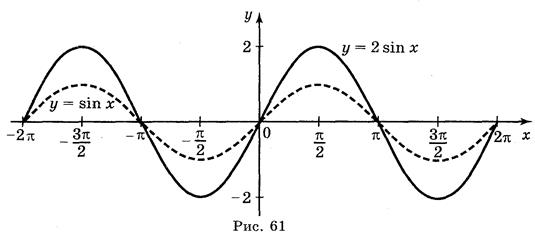
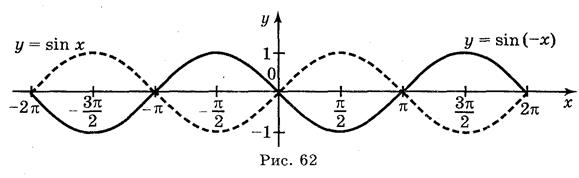
а) у = sin 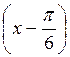; б) у = sin 2х; в) у = 2sin х; г) у = sin (-x).

Ответы: а) рис. 59; б) рис. 60; в) рис. 61; г) рис. 62.

III. Построение графика функции у = cos x

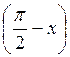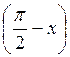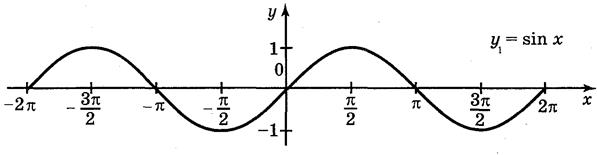
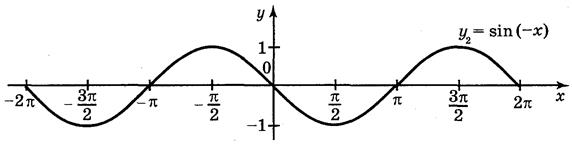
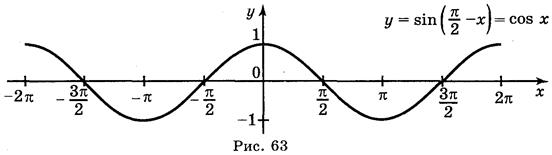
Как известно, cos х = sin , поэтому у = cos x и у = sin - одинаковые функции. Для построения графика функции у = sin 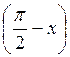воспользуемся геометрич-ими преобразованиями графиков: сначала построим (рис. 63) график функции у = sin х, затем у = sin (-х) и в конце у = sin .

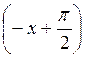Выполнение упражнений________________________________

1. Постройте графики функций:

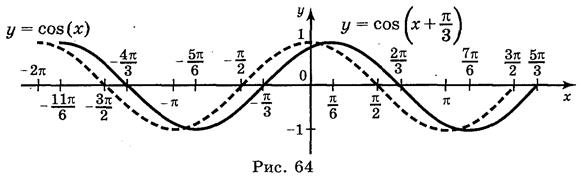
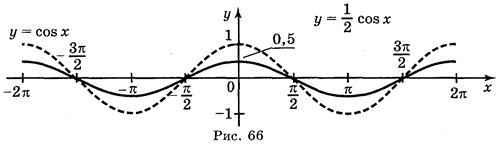
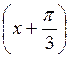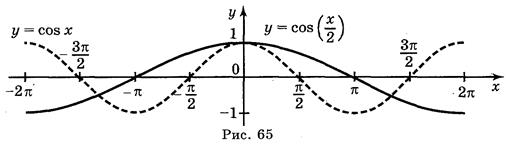
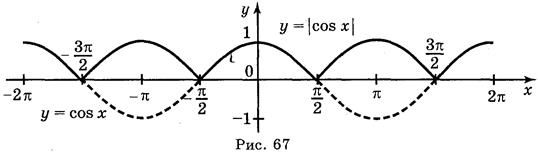
a) y = cos ; б) y = cos ; в) y =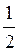 cos х; г) у = |cos x|.

Ответ: а) рис. 64; б) рис. 65; в) рис. 66; г) рис. 67.

IV. Построение графика функции у = tg x

График функции у = tg x построим с помощью линии тангенсов на промежутке 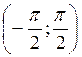, длина которого равна периоду π этой функции. Построим единичный круг радиусом 2 см (4 ячейки) и проведем линию тангенсов. Справа построим систему координат, как на рис. 68.

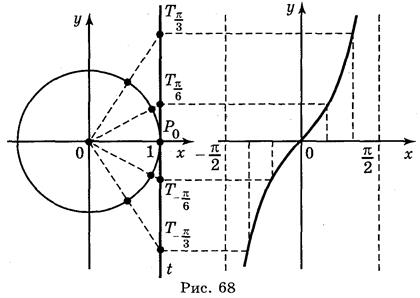
На ось ОХ нанесем точки 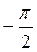; (6 ячеек). Разделим первую и четвертую четверть окружности на 3 равные части и на столько же частей каждый из отрезков 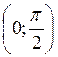и 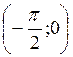. Найдем значения тангенсов чисел 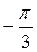; ; 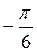0; ; с помощью линии тангенсов (ординаты точек 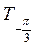; ; 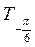; ; 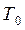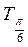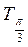линии тангенсов). Перенесем значения тангенсов до соответствующих точек оси ОХ. Последовательно соединив все полученные точки, получим график функции у = tg x на промежутке .

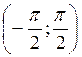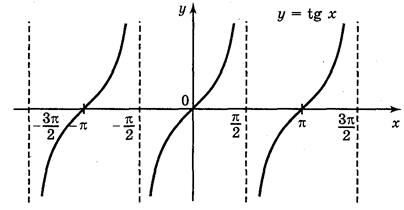
За то что функция у = tg x периодическая с периодом π, для построения графика функции у = tg x на всей прямой ОХ достаточно параллельно перенести построен график вдоль оси ОХ на π, 2π, 3π, 4π... единиц влево и вправо (рис. 69).

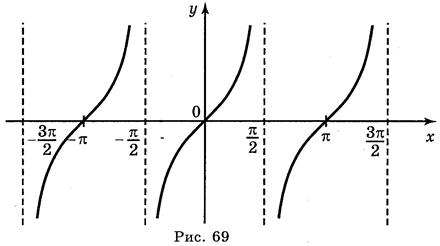
График функции у = tg x называется тангенсоїдою.

Выполнение упражнений

1. Постройте график функций

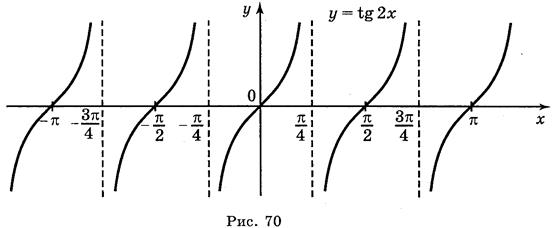
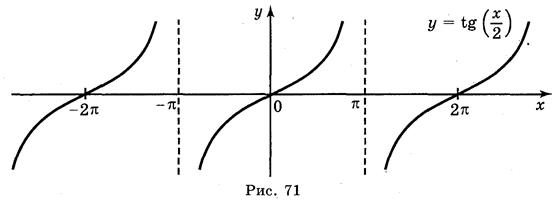
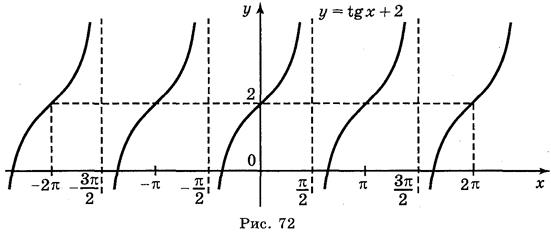
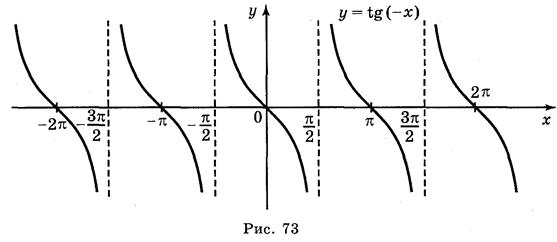
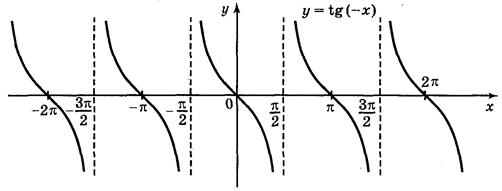
а) у = tg 2х; б) у = tgx; в) у = tg x + 2; г) у = tg (-x).

Ответы: а) рис. 70; б) рис. 71; в) рис. 72; г) рис. 73.

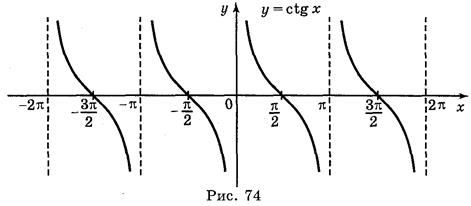
V. Построение графика функции у = ctg x

График функции у = ctg x легко получить, воспользовавшись формулой ctg x = tg 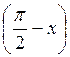и двумя геометрическими преобразованиями (рис. 74) симметрия относительно оси ΟΥ параллельный перенос вдоль оси ОХ на .

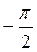IV. Домашнее задание

Раздел И § 6. Вопросы и задания для повторения раздела И № 50-51. Упражнения № 28 (а-г).

V. Итог урока