Градиент скорости материальной точки V со временем £ характеризуют ускорением

Ускорение выражается в метрах на секунду в квадрате (СИ) и сантиметрах на секунду в квадрате (СГС).

При прямолинейном движении вектор скорости направленный вдоль одной и той же прямой - траектории, вследствие чего направление вектора 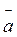совпадает с направлением вектора или противоположный него. Если 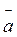совпадает по направлению с , то скорость увеличивается и движение будет ускоренным. Если 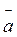противоположное по направлению к , то скорость уменьшается и движение будет замедленным.

Прямолинейное движение с постоянным ускорением называют рівнозмінним. В зависимости от изменения скорости во времени различают равномерно ускоренное и равномерно замедленное движения. При рівнозмінному прямолинейном движении справедлива формула

где - скорость в момент времени t; ₀- скорость в начальный момент времени (при t = 0); 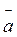- ускорение. При этом векторы , ₀, 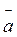направлены вдоль одной прямого.

Определим ускорение точки в случае ее движения по криволинейной траектории (рис. 1.2). Пусть в момент времени t точка была в положении А, а в момент времени t + Δt - в положении В. Скорости ₁и ₂ в точках А и В направлены по касательным к траектории в этих точках. Перенесем вектор ₂ в точку А. Изменение скорости за промежуток времени Δt определится вектором 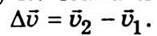С рис. 1.2. видим, что

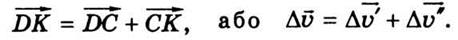
Тогда ускорение в точке А запишем так:

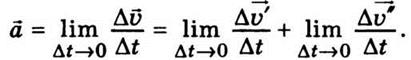
Вектор 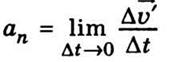называют нормальным ускорением, а вектор 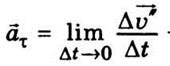- тангенциальным. Ускорение 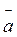_n перпендикулярное к вектору скорости ₁ и всегда напрямлене к центру кривизны. Отсюда и название этого вектора - нормальный (т.е. перпендикулярен).

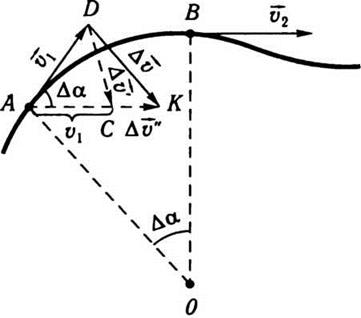
Рис. 1.2.

Определим модуль нормального ускорения. Как видно из рис. 1.2, для малого угла Δα можно записать

Тогда

Следовательно, модуль 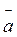_п в некоторой точке траектории равна отношению квадрата скорости к радиусу кривизны траектории в этой же точке:

Если на нормали к траектории отложить в точке А единичный вектор 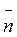, направленный к центру кривизны, то вектор нормального ускорения можно записать так:

Рассмотрим теперь вектор тангенциального ускорения

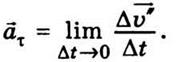
Отметим, что модуль вектора Δ’ равен по абсолютной величине разницы модулей ₂ и ₁ (см. рис. 1.2). Тогда

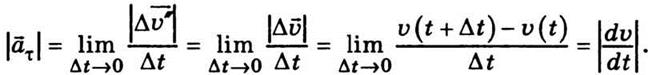
Соответственно тангенциальное ускорение

Следовательно, значение тангенциального ускорение равно первой производной от скорости по времени или второй похідній_від пути. Направление вектора 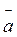_τ определяется направлением вектора Δ’, который он приобретает в предельном случае, когда Δt -> 0. Нетрудно увидеть, что в предельном случае вектор Δ’ направленный по касательной к траектории в точке А. Отсюда и название этого вектора - тангенциальный (касательный). Если ввести единичный вектор 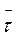, касательный к траектории и обращен в сторону движения точки, то вектор тангенциального ускорения можно записать так:

Вектор 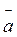_τ показывает, как изменяется скорость за числовым значением, а вектор 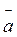_n характеризует изменение скорости по направлению. Следовательно, для полного ускорения запишем