Часть 1 МЕХАНИКА
Раздел 1 КИНЕМАТИКА
1.4. Движение точки по окружности
Движение материальной точки по окружности является
частным случаем криволинейного движения. Рассматривая такие величины, как скорость  , ускорение
, ускорение 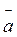 , радиус-вектор
, радиус-вектор 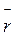 , вопрос о выборе их
напрямую не возникало, поскольку оно вытекало из их природы. Подобные векторы
называют полярными. Векторы типа dφ, направление которых связано с направлением
вращения, называют аксиальными. В этом случае угол можно рассматривать как вектор.
Для очень малых углов поворота Δφ, поскольку путь, который проходит
материальная точка при таком малом повороте, можно рассматривать как
прямолинейный.
, вопрос о выборе их
напрямую не возникало, поскольку оно вытекало из их природы. Подобные векторы
называют полярными. Векторы типа dφ, направление которых связано с направлением
вращения, называют аксиальными. В этом случае угол можно рассматривать как вектор.
Для очень малых углов поворота Δφ, поскольку путь, который проходит
материальная точка при таком малом повороте, можно рассматривать как
прямолинейный.
Величину

где
Δt - время, за которое совершается поворот
на угол Δφ, называют угловой скоростью точки.
Вектор 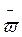 направленный
вдоль оси, вокруг которой вращается тело. Направление вращения определяется по правилу
правого винта. Угловая скорость - это аксиальный вектор. Модуль вектора угловой
скорости равна
направленный
вдоль оси, вокруг которой вращается тело. Направление вращения определяется по правилу
правого винта. Угловая скорость - это аксиальный вектор. Модуль вектора угловой
скорости равна 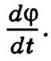 Вращения с постоянной угловой
скоростью называют равномерным, при этом ω
= φ/t. Следовательно, при равномерном вращении ω показывает, на какой угол поворачивается
тело за единицу времени.
Вращения с постоянной угловой
скоростью называют равномерным, при этом ω
= φ/t. Следовательно, при равномерном вращении ω показывает, на какой угол поворачивается
тело за единицу времени.
Равномерное движение можно
характеризовать периодом Т. Это время, в течение которого тело совершает один оборот,
т.е. поворачивается на угол 2π. Поскольку промежутка времени Δt = Т соответствует угол 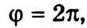 то
то

Частота периодического процесса

Тогда

Вектор 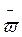 может меняться как в результате изменения
скорости вращения тела вокруг оси (в этом случае он изменяется по длине),
так и за счет поворота оси вращения в пространстве (в этом случае
может меняться как в результате изменения
скорости вращения тела вокруг оси (в этом случае он изменяется по длине),
так и за счет поворота оси вращения в пространстве (в этом случае 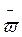 изменяется по
направлению). Пусть за время Δt вектор и получил прирост Δ
изменяется по
направлению). Пусть за время Δt вектор и получил прирост Δ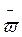 . Изменение вектора угловой скорости с
время характеризуют угловым ускорением
. Изменение вектора угловой скорости с
время характеризуют угловым ускорением

Вектор 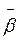 , как и
, как и 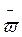 , является аксиальным. Если направление оси
вращения в пространстве остается постоянным, то угловая скорость изменяется только по
числовым значением и |Δ
, является аксиальным. Если направление оси
вращения в пространстве остается постоянным, то угловая скорость изменяется только по
числовым значением и |Δ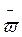 | = Δ.
В этом случае из формулы (1.17) получим
| = Δ.
В этом случае из формулы (1.17) получим

Выражение (1.18) запишем в векторной
форме

где
β - алгебраическая величина, которая
положительная, если ω со временем увеличивается (в этом случае
векторы (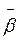 и
и 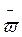 имеют
одинаковое направление), и отрицательная, если и уменьшается (в этом случае направления
имеют
одинаковое направление), и отрицательная, если и уменьшается (в этом случае направления 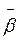 и
и 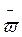 противоположны).
противоположны).
Линейная скорость υ определяется угловой скоростью
вращения тела ω и расстоянием r материальной точки от оси
вращения. Пусть за малый промежуток времени Δt тело поворачивается на угол Δφ. Точка, которая размещается на
расстоянии r от оси, проходит при этом путь

Линейная скорость точки
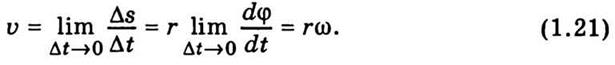
В векторной форме  = [
= [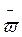 ,
,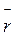 ]. Следовательно, чем дальше размещается точка
оси вращения, тем с большей линейной скоростью она движется.
]. Следовательно, чем дальше размещается точка
оси вращения, тем с большей линейной скоростью она движется.
Найдем связь модулей линейного
и углового ускорения, полагая, что r = const. Тогда, исходя из (1.18), запишем
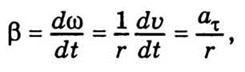
следовательно,

При равномерном движении точки по окружности
модуль скорости остается постоянным, но направление ее непрерывно меняется.
Рассмотрим два вектора скорости тела через небольшой промежуток времени Δt. Вычитая первое значение скорости  1 от следующего
1 от следующего  2, получим
прирост Δ
2, получим
прирост Δ (рис. 1.3). По общему правилу действия
над векторами можно перенести начало векторов скорости в одну точку (параллельное
перенос). Направление этих векторов совпадает с направлением касательной к окружности в той
точке, где лежит точка в определенный момент. Вектор Δ
(рис. 1.3). По общему правилу действия
над векторами можно перенести начало векторов скорости в одну точку (параллельное
перенос). Направление этих векторов совпадает с направлением касательной к окружности в той
точке, где лежит точка в определенный момент. Вектор Δ не будет перпендикулярным ни к
не будет перпендикулярным ни к  1, ни к
1, ни к  2. Однако при Δt -> 0 и Δ
2. Однако при Δt -> 0 и Δ -> 0 направление вектора Δ
-> 0 направление вектора Δ становится перпендикулярным к вектору скорости
становится перпендикулярным к вектору скорости
 .
.
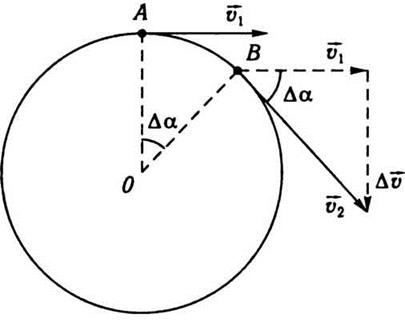
Рис. 1.3.
Следовательно, бесконечно малый прирост
вектор d перпендикулярен к вектору
перпендикулярен к вектору  , поэтому ускорение
, поэтому ускорение 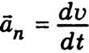 перпендикулярное
к скорости и напрямлене к центру круга. Значение ускорения можно связать
со значением скорости
перпендикулярное
к скорости и напрямлене к центру круга. Значение ускорения можно связать
со значением скорости  движения тела по окружности и значением радиуса r. При малом Δφ
движения тела по окружности и значением радиуса r. При малом Δφ

где
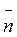 ’ - единичный вектор, направление которого
совпадает с направлением вектора Δ
’ - единичный вектор, направление которого
совпадает с направлением вектора Δ . Подставляя в (1.23) Δφ из (1.20), получим
. Подставляя в (1.23) Δφ из (1.20), получим

Разделив на Δt правую и левую части (1.24) и сделав соответствующие
преобразования, получим
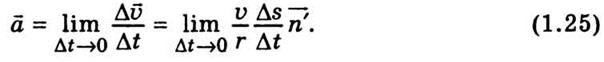
В этом выражении υ и r - стали, отношение 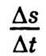 в предельном случае дает модуль
скорости υ; единичный вектор
в предельном случае дает модуль
скорости υ; единичный вектор 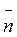 ’ в предельном случае совпадает с единичным вектором
’ в предельном случае совпадает с единичным вектором 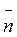 , перпендикулярным
к окружности в точке А и обращен к центру. Следовательно,
, перпендикулярным
к окружности в точке А и обращен к центру. Следовательно,

Найденное ускорение напрямлене
вдоль нормали к траектории, то есть оно является нормальным.
Если материальная точка движется по
окружности неравномерно, то кроме нормального (в случае движения по кругу называют еще
центростремительным) она будет иметь тангенциальное ускорение

которое
характеризует изменение скорости по числовым значением. Учитывая выражение (1.21),
для тангенциального ускорения получим

Следовательно, тангенциальное ускорение
растет линейно с увеличением расстояния от оси вращения. Окончательно для
вектора ускорения (рис. 1.4) запишем

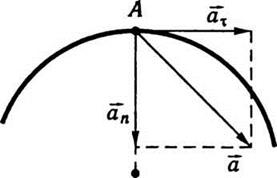
Рис. 1.4