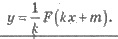МАТЕМАТИКА

ПРОПОРЦИИ. ПРОЦЕНТЫ

Правила нахождения первообразных

Правило 1. Если функции у = f(x) и у = g(x) имеют на числовом промежутке X первобытные, соответственно у = F(x) и у = G(x), то и сумма функций у = f(x) + g(x) имеет на промежутке X первоначальную в= =F(x) + G(x). (Первообразная суммы равна сумме первообразных.)

Правило 2. Если функция y = f(x) имеет на числовом промежутке X первоначальную y = F(x), то функция у = kf(x), где k - константа, имеет на промежутке X первоначальную y = kF(x). (Постоянный множитель можно вынести за знак первообразной.)

Правило 3. Если y = F(x) - первообразная для функции у = f(х), то первоначальной функции y = f(kx + m), где k и m - константы, служит функция