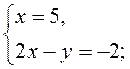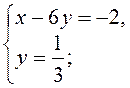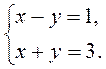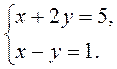|
@ После проведения самостоятельной работы - самопроверка и коррекция задач.
III. Формулировка задач и цели урока @ Осознания цели урока можно осуществить, если обратиться к схеме, показывает логическую взаимосвязь между основными содержательными линиями курса алгебры 7-9 классов.
Итак, после работы со схемой, учащиеся осознают, что знакомство с системами уравнений с двумя переменными и способами их решения было необходимо лишь для того, чтобы достать определенную «оружие» для решения важнейшего - решение текстовых задач.
IV. Актуализация опорных знаний Выполнение устных упражнений 1. Является ли решением системы 1) х = - 2; в= 1; 2) (0; 0); 3) (2; 1)? 2. Решите систему уравнений наиболее рациональным способом:
3. Составьте равенство, что соответствует условию: 1) Тетрадь стоит х к, записная книжка в к, вместе они стоят 2 грн. 30 к. 2) Тетрадь стоит х к, записная книжка у к. Записная книга дороже тетради на 1 грн. 60 к. 3) Тетрадь стоит х к, записная книжка стоит в к, три тетради и две записных книжки стоят 7 грн. 20 к. 4) Тетрадь стоит х к, записная книжка у к. Две записные книжки на 5 грн. дороже по три тетради.
V. Усвоение умений @ Во время ознакомления с технологией решения текстовых задач составлением систем линейных уравнений желательно показать ученикам, что способы действий почти не отличаются от тех способов, которые были ими использованы при решении текстовых задач на составление уравнения с одной переменной. То есть и виды задач (арифметические, на движение, на изменение величин и стоимость товара), и последовательность действий [а) обозначение неизвестных; б) использование условия задачи для составления уравнения математической модели задачи и решения уравнения; в) толкование найденных корней уравнения согласно условия задачи] остаются почти такими же, только добавляется обозначение еще одной неизвестной величины и составления и решения системы двух уравнений изученными способами. Как и на предыдущих уроках, ознакомление с технологией проводится на примере решения задачи. Чтобы целесообразность решения задачи составлением системы уравнений была обоснованной, можно предложить учащимся решить задачу сначала, составив одно уравнение, а затем предложить составить систему и привлечь учащихся к сравнение полученных решений. Схема решения задач составлением системы уравнений может быть записана учениками.
@ На первом уроке темы желательно обратиться к самым простым, с точки зрения учеников, задач - арифметических и геометрических. Обязательно требуем от учащихся сознательного выполнения действий в соответствии с алгоритмом решения задач. Во время решения задач постепенно приучаем учащихся к самоконтролю: проверки реальности ответа; проверки по содержанию задачи; проверки выполнения отдельных условий задачи. Выполнение письменных упражнений 1. Сумма двух чисел 13, а их разность 2. Найдите эти числа. 2. Надо разложить 163 шарики в два ящика так, чтобы в одном из них шариков стало в 2 раза больше, чем в другом. Сколько шариков нужно положить в каждый ящик? 3. Половина третьего числа равна трети второго, а треть первого числа на 5 меньше четверти второго. Найдите эти числа. 4. Периметр прямоугольника 30 м, а его длина больше ширины на 1 м. Найдите длины сторон прямоугольника. 5. Периметр равнобедренного треугольника равен 117 г. Боковая сторона на 13,2 м больше за основу. Найдите стороны треугольника.
VII. Итоги урока Составьте задачу, которую можно было бы решить, составив систему
VIII. Домашнее задание № 1. Изучите схему решения задач составлением системы уравнений. № 2. Используя схему, решите задачи: 1) В фермерское хозяйство было направлено 187 тракторов и комбайнов (вместе), причем комбайнов на 23 меньше, чем тракторов. Сколько тракторов и сколько комбайнов было направлено в хозяйство? 2) Сумма двух чисел равна 104. Одно из них на 11 больше от второго. Найдите эти числа. 3) Боковая сторона равнобедренного треугольника на 11 см меньше основы. Найдите основание треугольника, если периметр равен 68 см.
|
|
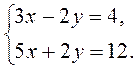
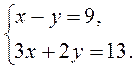
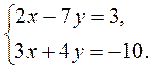
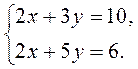
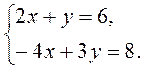
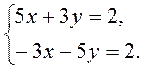

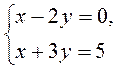 пара чисел:
пара чисел: