Урок № 7

Тема. Решение задач

Цель: дополнить знания учащихся понятиями: «достаточное и необходимое условия», «критерий»; отработать умения отличать необходимые и достаточные условия, а также использовать изучены необходимые и достаточные условия параллелограмма к решению задач.

Тип урока: применение знаний, умений и навыков.

Наглядность и оборудование: конспект «Параллелограмм».

Ход урока

I. Организационный этап

II. Проверка домашнего задания

Качество усвоения теоретического материала предыдущего урока можно проверить во время фронтальной беседы (которую можно провести в форме интерактивного упражнения «Микрофон»).

Вопросы для беседы

1. Диагонали четырехугольника АВКМ пересекаются. Обязательно ли этот четырехугольник является параллелограммом?

2. Точка пересечения диагоналей четырехугольника ВСКМ не является серединой одной из них. Может ли этот четырехугольник быть параллелограммом?

3. Точка М является серединой отрезка КО и BD. Как называется четырехугольник BKDО?

4. Отрезки MN и КР параллельны. Означает ли это, что четырехугольник MNKP является параллелограммом?

5. Для четырех точек плоскости А, В, С, К выполняется условие АВ =СК. Следует ли из этого условия вывод, что точки А, В,С, К являются вершинами параллелограмма?

6. Какие сведения необходимо иметь четырехугольник, чтобы сделать вывод о том, что он не является параллелограммом?

Проверка выполнения письменных упражнений проводится учителем фронтально по образцам (в случае необходимости) или только у тех учеников, которые требуют дополнительного педагогического внимания.

III. Формулировка цели и задач урока

Обратившись к таблице 1 (см. Геометрия в таблицах Есть. П. Нелина), учащиеся осознают, что все утверждения, касающиеся общего понятия параллелограмма, они изучили. После этого уместно будет еще раз обратиться к конспекту «Параллелограмм» и сравнить утверждения, выражающие свойства и признаки параллелограмма (см. таблицу). В этом случае велика вероятность того, что ученики заметят (если этого не произошло ранее), что свойства и признаки параллелограмма являются обратными утверждениями. Поэтому общую цель урока можно сформулировать как необходимость выяснения логической связи между изученными свойствами и признаками параллелограмма, а также дальнейшее формирование умений применять изученные утверждение о параллелограмм во время решения задач.

IV. Актуализация опорных знаний

Выполнение устных упражнений

1. В четырехугольнике ABCD A = 30°, C = 50°. Может ли данный четырехугольник быть параллелограммом? Какова особенность параллелограмма (свойство или признак) используется для решения этой задачи?

2. ABCD - параллелограмм, М - середина ВС, N - середина AD (рис. 1). Докажите, что АМСН - параллелограмм.

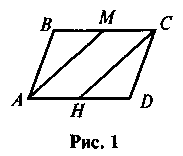
3. ABCD - параллелограмм, AM = СН (рис. 2). Докажите, что DHBM - параллелограмм.

4. На рисунке 3 АВ = CD, 1 = 2. Докажите, что ABCD - параллелограмм.

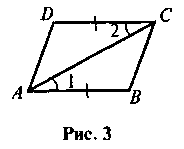
5. АВСD - параллелограмм, ВМ 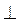АD, DH 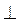BС (рис. 4). Докажите, что ΔABM = ΔCDH.

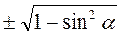
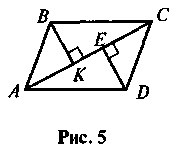
6. ABCD - параллелограмм, BK 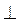AC, DE 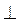AC (рис. 5). Докажите, что ВК = DE.

V. Усвоение новых знаний

План изучения нового материала

1. Достаточное условие.

2. Необходимое условие.

3. Геометрическое представление о критерий.

@ Хотя теоретический материал не является обязательным, изучение вопроса о необходимое и достаточное условие желательно провести на этом уроке, поскольку правильное представление учащихся о видах математических утверждений является одним из условий высокого уровня их математической культуры, а также залогом глубокого понимания общих математических закономерностей.

Изучение нового материала, которое можно провести за учебником, желательно закончить выполнением ряда упражнений на проверку понимания рассматриваемых понятий, использовав при этом не только материал, изученный на уроках геометрии в 8 классе, но и геометрический материал 7 класса, а также сведения из других областей знаний (физики, биологии и т.д.).

VI. Формирование первичных умений

Сознательному пониманию содержания понятия «необходимое и достаточное условия» будет способствовать решению устных упражнений.

Выполнение устных упражнений

1. Поставьте вместо точек слова «необходимо», «достаточно» или «необходимо и достаточно», чтобы утверждение было правильным.

а) Для того чтобы четырехугольник был параллелограммом, ..., чтобы его диагонали точкой пересечения делились пополам.

б) Для того чтобы два углы были смежными, ..., чтобы их сумма равна 180°.

в) Для того чтобы прямые АВ и CD были параллельными, ..., чтобы четырехугольник ABCD был параллелограммом.

С целью дальнейшего закрепления знаний и отработки умений применение признаков и свойств параллелограмма целесообразно письменно решить следующие задачи.

Выполнение письменных упражнений

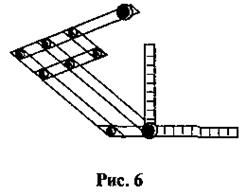
1. В техническом черчении для построения параллельных прямых используют механическую рейсшину (рис. 6). Объясните принцип ее действия.

2. В паралелограмі ABCD биссектрисы углов В и D пересекают диагональ АС в точках Е и F соответственно. Докажите, что четырехугольник BEDF - параллелограмм.

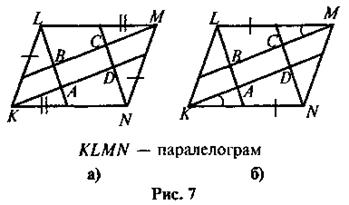
3. Заданными рисунка 7 докажите, что ABCD - параллелограмм.

4* (опорная). Если в четырехугольнике противоположные углы попарно равны, то этот четырехугольник - параллелограмм. Докажите.

VИI. Итоги урока

Самостоятельная работа (теоретическая)

Вариант 1

1. Существует ли четырехугольник, углы которого равны 100°, 80°, 135°, 55°?

2. В четырехугольнике ABCD A = С. Правильно, что ABCD - параллелограмм?

3. В паралелограмі ABCD A + C > 180°. Назовите острые углы параллелограмма.

4. Диагонали четырехугольника KLMN пересекаются в точке О, KL = MN, KL || MN. Назовите пары равных отрезков с общим концом В. Ответ обоснуйте.

Вариант 2

1. Существует ли четырехугольник, углы которого равны 20°, 150°, 10°, 180°?

2. В четырехугольнике ABCD AB = CD. Правильно, что ABCD - параллелограмм?

3. В паралелограмі ABCD B + D 180°. Назовите тупые углы параллелограмма.

4. Диагонали четырехугольника CDEF пересекаются в точке О, DE || CF, CD || EF. Назовите пары равных отрезков с общим концом В. Ответ обоснуйте.

Вариант 3

1. Существует ли четырехугольник, у которого три угла тупые и один прямой?

2. Правильно ли, что если в четырехугольнике две стороны параллельны, а две другие стороны равны, то этот четырехугольник - параллелограмм?

3. В паралелограмі ABCD с периметром Р ВС + AD + CD > 0,5 Г + АВ. Сравните стороны ВС и CD.

4. Сколько различных параллелограммов можно достать из четырех одинаковых параллелограммов, если прикладывать их друг к другу разными способами?

Вариант 4

1. Существует ли четырехугольник, у которого три угла острых и один прямой?

2. Правильно ли, что если в четырехугольнике есть две пары равных, не обязательно противоположных сторон, то этот четырехугольник - параллелограмм?

3. В паралелограмі ABCD с периметром Р 0,5P + CD > BC + AD + AB. Сравните стороны ВС и АВ.

4. Сколько различных параллелограммов можно достать из двух равных равнобедренных, но не равносторонних треугольников, если прикладывать их друг к другу разными способами?

VIII. Домашнее задание

Повторить теоретические сведения о параллелограмм. Выполнить домашнюю самостоятельную работу.

Домашняя самостоятельная работа

1. Один из углов параллелограмма равен 47°. Найдите остальные углы.

2. Периметр параллелограмма равен 112 см, а две его стороны относятся как 5 : 3. Найдите стороны параллелограмма.

3. Угол между биссектрисой тупого угла параллелограмма и высотой, проведенной из вершины этого угла, равна 40°. Найдите углы параллелограмма.

4. Биссектриса одного из углов параллелограмма делит его сторону пополам. Найдите периметр параллелограмма, если эта сторона равна а см.