УРОК № 7

Тема. Теорема синусов

Цель урока: изучение теоремы синусов. Формирование умений учащихся применять изученную теорему к решению задач.

Тип урока: комбинированный.

Наглядность и оборудование: таблица «Соотношение между сторонами и углами треугольника» [13].

Требования к уровню подготовки учащихся: формулируют теорему синусов и доказывают ее.

Ход урока

И. Проверка домашнего задания

Проверить правильность выполнения домашних заданий по записям с пробелами.

Коллективно обсуждается ход решения задач и вписываются соответствующие символы (записи). Там, где стоит знак (?), необходимо объяснить, сделать ссылки на соответствующие теоремы.

1. 1) Пусть АС = с, BD = d, AOB = α (рис. 21). Поскольку ABCD - параллелограмм, то АО=..., = ... (?).

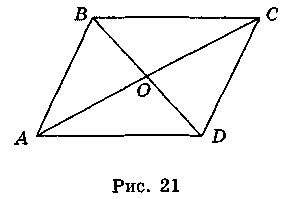
По теореме косинусов:

АВ2 = АО2 + ВО2 - 2АО ∙ ВО ∙ cos AOB = ... + ... - ... .

BOC = 180° - α (?).

ВС2 = ВО2 + СО2 - 2Х ∙ CO ∙ cos BOC = ... + ... - ... .

Ответ. , .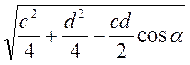

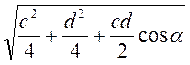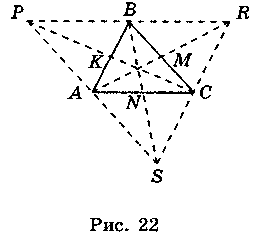
1. 2) Пусть АВ = 5 м, BC = 6 м, АС = 7 м (рис. 22). АВRC - параллелограмм. (?)

AR2 + BC2 = 2(AB2 + AC2) (?) 4АМ2 = - 36 + 2 ∙ (25 + 49) (?)

АМ2 = ..., АМ = .... АРВС - параллелограмм. (?)

4СK2 + АВ2 = 2 ∙ (AC2 + BC2) (?) СК2 = ..., СК = ....

ABCS - параллелограмм. (?) 4BN2 + ... = 2 ∙ (... + ...).

ВМ2 = ..., ВМ = ....

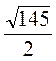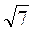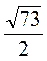Ответ. м, 2 м, м.

Самостоятельная работа

Вариант 1

1. 1. В треугольнике один из углов составляет 60°, а стороны, прилегающие к нему, равны a и b. Найдите третью сторону треугольника. (4 балла)
2. 2. Стороны параллелограмма равны 32 см и 10 см, а угол между ними составляет 120°. Найдите диагонали параллелограмма. (4 балла)
3. 3. Найдите диагонали параллелограмма, если они относятся как 3 : 5, а длины сторон равны 8 см и 19 см. (4 балла)

Вариант 2

1. 1. В треугольнике две стороны равны a и b, а угол между ними составляет 120°. Найдите третью сторону треугольника. (4 балла)
2. 2. Диагонали параллелограмма равны 32 см и 10 см, а угол между ними составляет 60°. Найдите стороны параллелограмма. (4 балла)
3. 3. Стороны параллелограмма относятся как 1 : 2. Найдите стороны параллелограмма, если его диагонали равны 18 см и 26 см. (4 балла)

Ответы к заданиям самостоятельной работы

Вариант 1. 1. a2 + b2 - ab.

2. 38 см и 2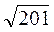см. 3. 15 см и 25 см.

Вариант 2. 1. a2 + b2 + ab.

2. 19 см и 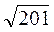см. 3. 10 см и 20 см.

II. Восприятие и осознание нового материала

Изучение теоремы синусов

Приводим объяснение теоремы синусов.

Рассмотрим прямоугольный треугольник ABC (рис. 23).

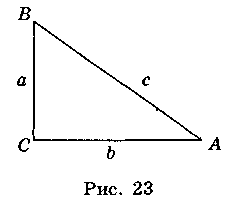
Известно, что а = c sinA, b = c sinB, отсюда 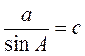, 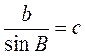. Тогда 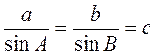. Учитывая, что C = 90° и sinC = 1, запишем: .

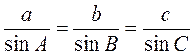Если описать круг радиуса R вокруг прямоугольного треугольника ABC (рис. 24), то получим: .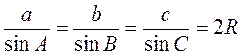

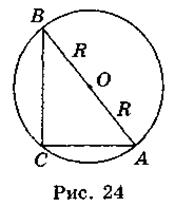
Следовательно, в прямоугольном треугольнике стороны пропорциональны синусов противоположных углов.

А есть ли это утверждение правильным для любого треугольника?

Сначала выясним соотношение между диаметром круга, стороной вписанного в него треугольника и углом треугольника, противоположной этой стороне.

Пусть в треугольнике ABC угол А острый, ВС = а (рис. 25). Проведем диаметр BD, равный 2R, R - радиус описанного круга.

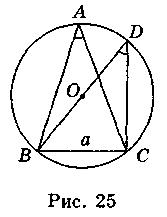
Соединив точки D и С, получим прямоугольный треугольник BDC, в котором ВС является катетом, и поэтому BC = BD sinD. Но D = А как вписанные, опирающиеся на дугу ВС, и поэтому sinD = sinA.

Следовательно, a = 2R sinA.

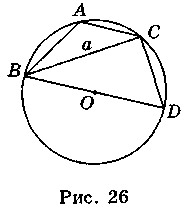
Полученное соотношение выполняется и тогда, когда угол А тупой (рис. 26), поскольку A + D = 180°. Тогда D = 180° - A и sinD = sin(180°- А). Таким образом, а = ВС = BD sinD = 2R sinD = 2R sinA.

Следовательно, всегда a = 2R sinA.

Аналогично убеждаемся, что b = 2R sinB, c = 2R sinC. В каждой из трех последних равенств выразим отношение стороны к синусу противоположного угла:

; ; .

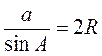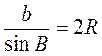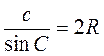Следовательно, .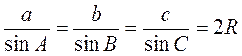

Таким образом, стороны треугольника пропорциональны синусов противоположных углов, отношение стороны треугольника к синусу противоположного угла равно диаметру окружности, описанной вокруг треугольника.

Решение задач

1. 1. Сторона треугольника равна 20 см, а противоположный угол равен 150°. Найдите радиус круга, описанного вокруг треугольника. (Ответ. 20 см)
2. 2. Найдите сторону АВ треугольника ABC, если ВС = 2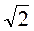см, A = 45°, C = 30°. (Ответ. 2 см)

III. Закрепление и осмысление изученного материала

Коллективное решение задачи

1) В треугольнике ABC АВ = 15 см, АС = 10 см. Может sinβ = ?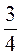

Решение

Предположим, что sinβ = 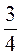. Тогда из равенства 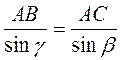, учитывая, что АВ = 15 см, АС = 10 см, получим: 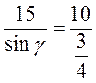. Отсюда sinγ = 15 ∙ 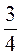∙ 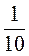= 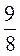> 1, что невозможно (потому sinγ 1).

Итак, sinβ не может равняться .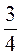

Ответ. Не может равняться.

2) В треугольнике заданы две стороны a = 27, b = 9 и угол, противоположный одной из сторон, α = 138°. Найдите остальные два угла и третью сторону треугольника.

Решение

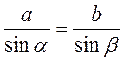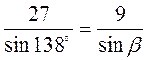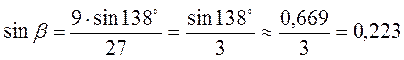; ; ; β 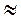13°. Тогда γ = 180° - α - β 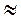180° - 138° - 13° = 29°.

; ; .

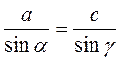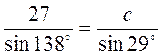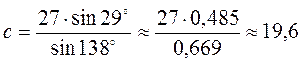Ответ. β 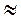13°, γ 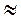29°, с 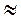19,6.

Задачи для индивидуального решения

1. 1) В рівнобедреному треугольнике основание равно а, а угол при основании равен 2β. Найдите бісектрису треугольника, проведенную к боковой стороне.

Ответ. .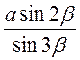

1. 2) В прямоугольном треугольнике гипотенуза равна с, а один из острых углов равен α. Найдите бісектрису прямого угла.

Ответ. .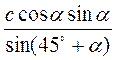

1. 3) Докажите, что сторона треугольника, лежащая против угла в 30°, равна радиусу круга, описанного вокруг этого треугольника.
2. 4) Докажите, что биссектриса угла треугольника делит противоположную сторону на отрезки, обратно пропорциональные синусам прилегающих к этой стороне углов.

Доведение

Пусть в треугольнике ABC (рис. 27) BD - биссектриса и ABD = DBC = x.

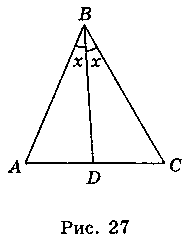
Из треугольника ABD по теореме синусов имеем: 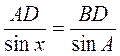. (1)

Из треугольника BDC по теореме синусов имеем: 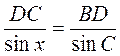. (2)

Разделив равенство (1) на равенство (2), получим 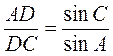, что и требовалось доказать.

IV. Домашнее задание

1. 1. Изучить теорему синусов.
2. 2. Решить задачу.

В треугольнике даны две стороны и угол, противоположный к одной из сторон. Найдите остальные два угла и третью сторону треугольника, если:

а) а = 12, b = 5, α = 120°;

б) а = 34, b = 12, α = 164°.

V. Подведение итогов урока

Задание к классу

1. 1. Сформулируйте теорему синусов.
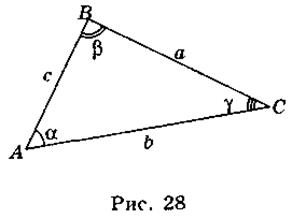
2. 2. В треугольнике ABC (рис. 28) стороны равны a, b, c, a углы равны α, β, γ. Вокруг этого треугольника описана окружность радиуса R. Какие из приведенных утверждений являются правильными, а какие - неправильными?

a) b = 2R sinα;

б) ;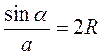

в) ;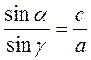

г) 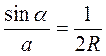.