Урок 7

Тема. Взаимное расположение двух прямых в пространстве

Цель урока: изучение взаимного расположения двух прямых в пространстве: прямые, которые пересекаются; параллельные прямые; скрещивающиеся прямые. Формирование понятий: параллельные прямые, скрещивающиеся прямые.

Оборудование: стереометрический набор, каркасная модель куба, схема “Взаимное расположение двух прямых в пространстве”.

Ход урока

И. Проверка домашнего задания

Проверку правильности выполнения домашней задачи провести путем фронтальной беседы с записями, сделанными на доске до начала урока.

Решение задачи

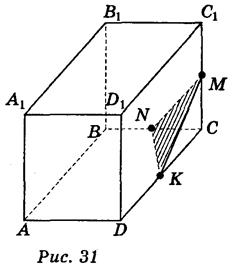
ABCDA1B1C1D1 - прямоугольный параллелепипед, в котором: AD = 6 см, DD1 = 6 см, DC = 8 cm (рис. 31).

СС1 = 2MC ; DC = 2CK; BC = 2NC .

ΔΜΝΚ - искомое сечение.

Из ΔMKC 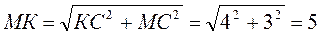(см).

Из ΔNCM 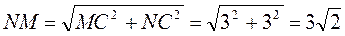(см).

Из ΔNKC 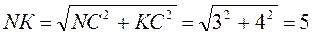(см).

PMNK = MN +NK+ MK = 10 + 3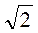 (см).

Ответ. 10 + 3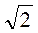 см.

Вопрос к классу

1) Объясните, что такое прямоугольный параллелепипед.

2) Как построено искомое сечение?

3) Почему треугольник МСК - прямоугольный?

4) Какова длина ребра CC1 ? Почему?

5) Какова длина ребра ВС? Почему?

6) Определите вид треугольника MNK.

II. Анализ самостоятельной работы, проведенной на предыдущем уроке

III. Восприятие и осознание нового материала

Взаимное расположение двух прямых в пространстве

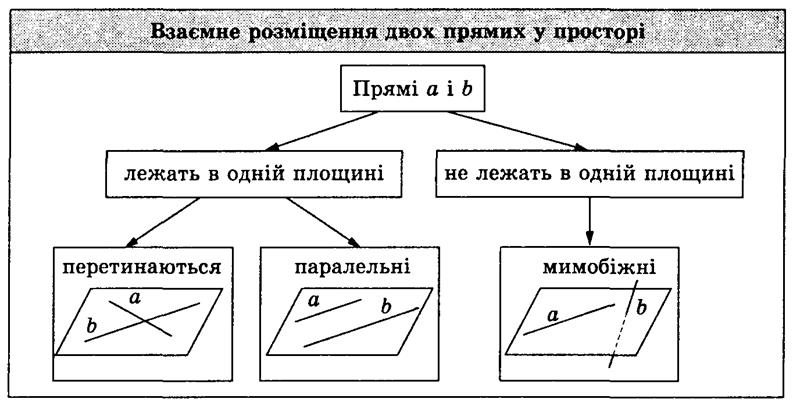
Из курса планиметрии известно, что две прямые, которые лежат в плоскости, могут пересекаться или не иметь общих точек. Если две прямые лежат в одной плоскости и не имеют общих точек, то они называются параллельными. В пространстве две различные прямые либо пересекаются, либо не пересекаются. Однако второй случай допускает две возможности: прямые лежат в одной плоскости или прямые не лежат в одной плоскости.

Прямые, которые не пересекаются и лежат в одной плоскости, называются параллельными, а две прямые, которые не пересекаются и не лежат в одной плоскости, называются скрещивающимися.

Случаи взаимного расположения двух прямых в пространстве демонстрируются с помощью стереометричного набора или на каркасной модели куба.

Итак, две прямые а и b в пространстве могут пересекаться, быть параллельными, быть скрещивающимися (демонстрируется схема, приведенная ниже).

Выполнение упражнений

1. Различные случаи расположения двух прямых в пространстве продемонстрируйте на предметах окружения.

2. Дано изображение куба ABCDA1B1C1D1 (рис. 32).

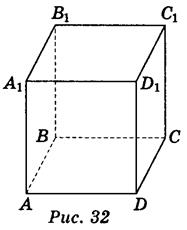
а) пересекаются Ли прямые АА1 и ВВ1? А1В1 и D1C1? Как называются эти прямые?

б) пересекаются Ли прямые AD и ВВ1? АВ и DD1? Как называются эти прямые?

в) можно Ли провести плоскость через прямые AD и DB1? A1D1 и C1D1? AD и ВВ1? АА1 и DВ1? АА1 и DD1?

3. Как расположены оси железнодорожных вагонов между собой; относительно рельсов?

4. Как надо понимать, что прямые а и b в пространстве не параллельны?

5. Что можно сказать о прямых а и b, если известно, что они не скрещивающиеся?

IV. Закрепление и осмысление знаний учащихся

Решение упражнений

1. Прямые АВ и CD параллельны. Могут быть скрещивающимися прямые АС и BD? А пересекаться?

2. Прямые АВ и CD скрещивающиеся. Могут быть прямые АС и BD параллельны? А пересекаться?

3. Задача № 2 из учебника (с. 18).

4. Задача № 3 из учебника (с. 18).

5. Κ, Ρ, Τ, Μ - середины ребер АВ, AC, CD, DB тетраэдра DABC. Найдите периметр четырехугольника КРТМ, если AD = 6 см, ВС = 8 см.

V. Домашнее задание

§1, п. 7 (до теоремы 2.1); контрольные вопросы № 1, 2; задача № 1 (с. 18).

VI. Подведение итога урока

Вопрос к классу

1) Как могут располагаться две прямые на плоскости?

2) Как могут располагаться две прямые в пространстве?