Часть 2 МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА

Раздел 7 ОСНОВЫ ТЕРМОДИНАМИКИ

7.2. Работа термодинамической системы

Пусть газ находится в цилиндре с легко-подвижным поршнем. Песок, насыпанный на поршень, поддерживает его в равновесии. При этом газ находится под давлением р = 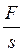, где F - вес песка и поршня; s - площадь поршня. Если повысить температуру газа на величину dТ или немного снять песок, то газ расширится и поршень переместится на расстояние dh. При этом давление газа можно считать устойчивым вследствие незначительного увеличения объема. Элементарная работа, которую выполняет газ при расширении.

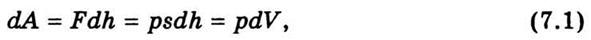
т.е. равна произведению давления на прирост объема. Такой же формуле будет определяться элементарная работа расширения произвольного тела, а не только газа, потому что при выводе формулы (7.1) мы не пользовались любыми особенностями газообразного состояния.

Если при повышении температуры от Т₁ до Т₂ объем увеличивается от V₁ до V₂, а давление остается постоянным, то работа будет

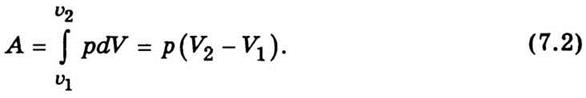
Следовательно, работа расширения ізобарного газа, то есть расширение за неизменного давления, равна произведению давления на прирост объема. Формулу (7.2) можно преобразовать, воспользовавшись уравнением состояния идеального газа для произвольной массы.

Запишем уравнение состояния идеального газа, масса которого m и молекулярная масса μ, до расширения:

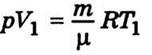
и после расширения:

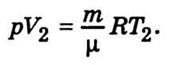
Отняв от второго уравнения соответственно левую и правую части первого уравнения, достанем

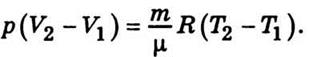
Принимая во внимание (7.2), имеем

Следовательно, работа расширения ізобарного идеального газа равна произведению универсальной газовой постоянной на повышение температуры и на число молей газа.

Из соотношения (7.3) можно понять физический смысл универсальной газовой постоянной: если m = μ, а Т₂ - Т₁ = 1, то R = А. Итак, универсальная газовая постоянная численно равна работе ізобарного расширения моля идеального газа при нагревании на один градус.

Аналитическое выражение работы изотермического расширения идеального газа получим так: по уравнению Менделеева - Клапейрон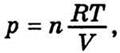а а элементарная работа dА = рdV, тогда

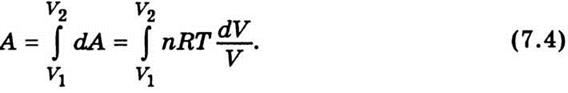
Поскольку Т = const, после интегрирования имеем

где n - число молей; V₁ и V₂ - начальный и конечный объемы соответственно. Соотношение (7.5) определяет работу изотермического расширения идеального газа.

Рассмотрим графическое изображение работы термодинамической системы. На рис. 7.2 подано ізобару идеального газа в координатной системе г - V. Точка В показывает исходное состояние, точка С - конечный.

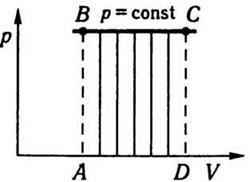
Рис. 7.2

Работа А ізобарного расширения вычисляется по формуле (7.2) и численно равна площади АВСDА под изобарой ВС.

Если расширения идеального газа от одного состояния к другому происходит изотермически, то работа изображается плоскостью под соответствующей частью изотермы, как показано на рис. 7.3. Следовательно, работа в этом случае определяется площадью, которая ограничена изотермой ВС, двумя ординатами (ВV₁ и СV₂), соответствующие начальному и конечному состояниям, и отрезком V₁ V₂ по оси абсцисс.

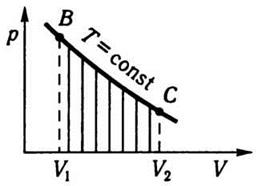
Рис. 7.3