Интересные упражнения

Тема. Преобразование целых выражений

1. Игровые моменты.

А) За 1 минуту записать как можно больше таких двочленів, чтобы в случае вынесения общего множителя за скобки в скобках осталось 2х - 3;

Б) За 1 минуту записать как можно больше таких дробей со знаменателем х(х - 2), которые можно сократить.

В) За 1 минуту придумайте как можно больше таких дробей, чтобы после их сокращения творения вся дробь .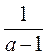

Г) Играют парами. У каждого из партнеров по 5-7 карточек. На каждой из карточек написано или одночлен, или двочлен. Первый кладет на стол любую карту, второй имеет под нее положить такую карточку, чтобы дробь, образовавшийся был скоротним; при нем говорит, на какой множитель сокращается дробь и что образуется после сокращения.

Затем партнеры меняются ролями.

Д) Учитель. Я задумал алгебраический дробь, и вы сможете отгадать его. Один из учеников записывает на доске любой дробь (для удобства будем использовать букву х), а я найду произведение этих дробей и запишу его.

Например, ученик записал дробь 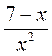; 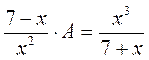. Который дробь я задумал?

2. Сумма двух дробей с одинаковыми знаменателями равна 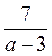, а разность - 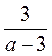. Которые эти дроби?

3. Вместо квадратиков запишите такие одночлен, чтобы равенство стало тождеством: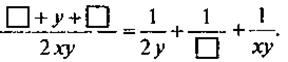

4. Найдите два одночлен, если их произведение равно (ab)12, а доля равна .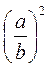

5. Вместо * поставьте такие знаки действий, чтобы равенство стало тождеством (можно использовать скобки): .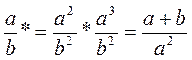

Тема. Квадратные корни

1. Дано 4 числа: 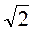; ; 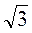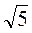и . И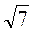з них составляют различные частицы, например 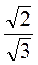; 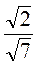и т. д.

1) Сколько таких частиц можно составить?

2) Найдите наименьшую и наибольшую долю.

3) Чему равно произведение всех долей?

2. 1) Запишите число 2 ровно двумя двойками, используя известные действия (можно скобки).

2) Запишите 6 раз число 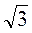и знаки действий, чтобы получившееся число 6.

3) Используя 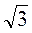и 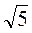по 2 раза, образуйте число 2.

3. Что больше: 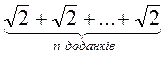или ?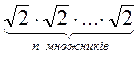

4. Придумайте такие два числа а и b, чтобы одновременно выполнялись три условия:

а) 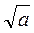и 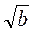- иррациональные числа;

б) 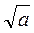· 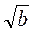- натуральное число;

в) 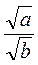- рациональное число.

5. Вместо х и у назовите такие натуральные числа, чтобы выполнялось неравенство 6 х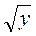 7.

6. Игровой момент.

На доске записаны 24 натуральные чистая: 2, 3, 4, ..., 23, 24, 25. Ученик должен назвать весь ряд по следующим правилам: показывая последовательно на число 2, говорит 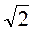и т. д. Если корень извлекается, то ученик называет значение корня. Если это число составное, то следует представить его в виде произведения корней. Например, 4 = 2; 6 = 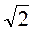·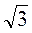, то есть под знаком корня должны быть только простые числа.

Кто сможет назвать весь ряд без ошибки?

7. Десять секунд на размышления.

На решение каждого из следующих задач попробуйте расходы ты не больше 10 секунд.

1) 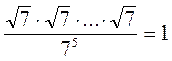. Сколько множителей в числителе?

2) Что больше: А или В, если , ?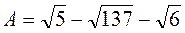

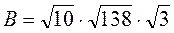3) Чему равно а, если 10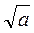= а?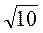

4) Вычислите: .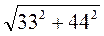

8. Игровой момент. Играют парами. Первый записывает число вида а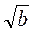, где а и b - натуральные числа, меньшие от 15, например 7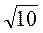. Второй должен записать число вида 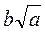, то есть 10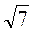. Числа сравниваются. Побеждает тот, у кого число получилось больше. Затем меняются ролями

9. Игровой момент.

Играют двое. Каждый записывает по одному положительном числу на листе бумаги. Затем первый находит среднее арифметическое этих чисел, а второй находит произведение и извлекает квадратный корень из произведения. Можно ли предсказать, кто пер может в этой игре?