УРОК № 65

Тема. Числовые последовательности

Тестовые задания

1. Последовательность задана формулой аn = 5n + 2. Найдите а3.

а) 3; б) 17; в) 5; г) другой ответ.

2. В арифметической прогрессии (bп) разность равна 2. Найдите b10, если b1 = 3.

а) 1536; б) 18; в) 21; г) другой ответ.

3. Найдите сумму первых пяти членов арифметической прогрессии (bn), если b1 = - 10, а разность равна 10.

а) 0; б) 50; в) 100; г) -100.

4. Чему может быть равен знаменатель геометрической прогрессии (bn), если b10 = 10; b12 = 40?

а) 2; б) ±2; в) 4; г) 15.

5. Чему равна сумма пяти первых членов геометрической прогрессии (bn), если b1 = 1, а знаменатель равен -2 ?

а) 11; б) -17; в) 17; г) другой ответ.

6. Найдите сумму бесконечной геометрической прогрессии (аn), если а1 = 3, а2 = 0,3.

а) 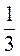; б) 3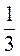; в) -3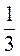; г) 1.

Письменные упражнения

1. Найдите разность арифметической прогрессии, первый член которой равен 10, а сумма первых 14-ти членов равна 1050.

2. Найдите сумму первых шести членов геометрической прогрессии (bn), если b2 = 12, b5 = -96.

3. Последовательность задана формулой хn = n2 - 3n + 1. Найдите номер члена этой последовательности, если он равен 19.

4. Запишите в виде обычного несократимый дроби число 0,3(2).

5. При каком значении х числа 3х - 1; х + 5 и x + 17 будут последовательными членами геометрической прогрессии?

6. Найдите сумму всех трехзначных чисел, меньших 250, кратные 3.