Урок 61
Тема. Тематическое оценивание № 6
Цель урока: проверка знаний учащихся по теме «Углы и векторы в пространстве».
Ход урока
Тематическое оценивание № 6 можно провести путем выполнения тематической контрольной работы.
И. Тематическая контрольная работа № 6
Вариант А
Вариант 1
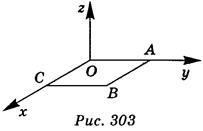
1. Сторона квадрата ОАВС равна 5 (рис. 303). Запишите координаты вектора 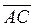 . (3 балла)
. (3 балла)
2. Из точки, удаленной от плоскости на расстоянии 10 см, проведены две наклонные, образующие с плоскостью углы в 45° и 30°. Угол между их проекциями равен 90°. Найти расстояние между концами наклонных. (3 балла)
3. Даны векторы 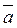 (4; -2; -4) и
(4; -2; -4) и 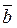 (6; -3; 2). Вычислите (
(6; -3; 2). Вычислите (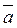 -
- 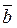 )2 и угол между векторами
)2 и угол между векторами 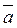 и
и 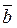 . (3 балла)
. (3 балла)
4. Ортогональной проекцией трапеции, площадь которой равна 80см2, есть равносторонняя трапеция с основаниями 7 и 13 см и боковой стороной 5 см. Вычислите угол между плоскостью трапеции и плоскостью ее проекции. (3 балла).
Вариант 2
1. Сторона квадрата ОАВС равна 5 (рис. 304). Запишите координаты вектора 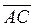 . (3 балла)
. (3 балла)
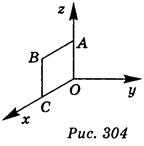
2. Из точки, удаленной от плоскости на расстоянии 10 см, проведены две наклонные, образующие с плоскостью углы в 30°, а между собой угол в 60°. Найдите расстояние между концами наклонных. (3 балла)
3. Даны векторы 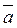 (4; -2; -4) и
(4; -2; -4) и 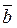 (6; -3; 2). Вычислите (
(6; -3; 2). Вычислите (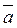 +
+ 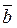 )2 и угол между векторами
)2 и угол между векторами 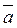 и
и 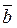 . (3 балла)
. (3 балла)
4. Ортогональной проекцией трапеции есть равносторонняя трапеция с основаниями 7 и 25 см и диагоналями, которые перпендикулярны к боковым сторонам. Угол между плоскостями этих трапеций равна 60°. Вычислите площадь данной трапеции. (3 балла).
Вариант 3
1. Сторона квадрата ОАВС равна 5 (рис. 305). Запишите координаты вектора 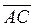 . (3 балла)
. (3 балла)
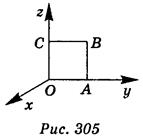
2. С точки, находящейся на расстоянии 6 от плоскости, проведены к этой плоскости две наклонные под углом 30° к ней. Их проекции образуют 120°. Найдите расстояние между концами наклонных. (3 балла)
от плоскости, проведены к этой плоскости две наклонные под углом 30° к ней. Их проекции образуют 120°. Найдите расстояние между концами наклонных. (3 балла)
3. Дано: 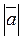 = 13,
= 13, 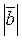 = 19,
= 19, 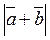 = 24 . Вычислите
= 24 . Вычислите 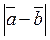 . (3 балла)
. (3 балла)
4. Ортогональной проекцией данного треугольника, площадь которого равна 36 см2, является прямоугольный треугольник, катет которого равен 12 см, а медиана, проведенная к гипотенузы, - 7,5 см. Вычислите угол между плоскостями этих треугольников. Может ли данный треугольник быть правильным? (3 балла).
см2, является прямоугольный треугольник, катет которого равен 12 см, а медиана, проведенная к гипотенузы, - 7,5 см. Вычислите угол между плоскостями этих треугольников. Может ли данный треугольник быть правильным? (3 балла).
Вариант 4
1. Сторона квадрата ОАВС равна 5 (рис. 306). Запишите координаты вектора 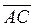 . (3 балла)
. (3 балла)
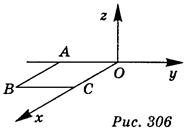
2. Из точки, удаленной от плоскости на 8 см, проведены две наклонные под углом 45° к плоскости. Найдите расстояние между основаниями наклонных, если угол между проекциями наклонных равен 120° . (3 балла)
3. Дано: 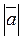 = 11,
= 11, 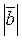 = 23,
= 23, 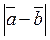 = 30. Вычислите
= 30. Вычислите 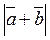 . (3 балла)
. (3 балла)
4. Ортогональной проекцией данного треугольника является прямоугольный треугольник, гипотенуза которого равна 15 см, а катет - 9 см. Угол между плоскостями этих треугольников равен 30°. Найдите площадь данного треугольника. Может ли данный треугольник быть правильным? (3 балла).
Ответ. Вариант 1. 1. 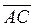 (5; -5; 0) . 2. 20 см. 3. (
(5; -5; 0) . 2. 20 см. 3. (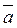 -
- 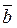 )2 = 41, arccos
)2 = 41, arccos 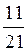 . 4. 60°.
. 4. 60°.
Вариант 2. 1. 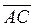 (5;0;-5). 2. 20см. 3. (
(5;0;-5). 2. 20см. 3. (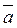 +
+ 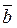 )2 = 129, arccos
)2 = 129, arccos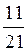 . 4. 384см2.
. 4. 384см2.
Вариант 3. 1. 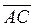 (0;-5;5). 2. 18
(0;-5;5). 2. 18 см. 3. 22. 4. 30°, не может.
см. 3. 22. 4. 30°, не может.
Вариант 4. 1. 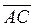 (5; 5; 0). 2. 8
(5; 5; 0). 2. 8 см. 3. 20. 4. 36
см. 3. 20. 4. 36 см2, не может.
см2, не может.
Вариант Б
Вариант 1
1. Даны точки А (1; 0; - 2), В (-2; 1; 3) и вектор 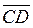 (1; 0; - 2) . Найдите:
(1; 0; - 2) . Найдите:
а) координаты вектора 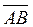 ; (2 балла)
; (2 балла)
б) абсолютную величину вектора 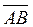 ; (2 балла)
; (2 балла)
в) координаты суммы векторов 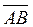 и
и 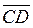 ; (2 балла).
; (2 балла).
2. Найдите длину вектора 2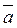 +3
+3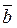 , если
, если 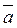 (3; 1; 0),
(3; 1; 0), 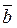 (0; 1; -1). (3 балла)
(0; 1; -1). (3 балла)
3. Найдите косинус угла С треугольника АВС, если А(0; 1; - 1), В (1; - 1; 2), С(3; 1; 0). (3 балла)
Вариант 2
1. Дано точки А(3; 2; 1), B(1; 2; 3) и вектор 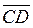 (1; 1; 1). Найдите:
(1; 1; 1). Найдите:
а) координаты вектора 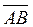 ; (2 балла)
; (2 балла)
б) абсолютную величину вектора 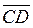 ; (2 балла)
; (2 балла)
в) координаты разности векторов 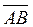 и
и 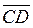 ; (2 балла).
; (2 балла).
2. Векторы 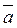 и
и 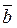 перпендикулярны, причем
перпендикулярны, причем 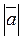 = 12,
= 12, 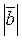 =16. Найдите
=16. Найдите 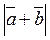 . (3 балла)
. (3 балла)
3. Найдите косинус угла А треугольника АВС, если А(0; 1; -1), В (1; -1; 2), С(3; 1; 0). (3 балла)
Вариант 3
1. Дан вектор 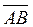 (1; 2; 3) и точки C (1; 0; 1) и D (1; 1; 2). Найдите:
(1; 2; 3) и точки C (1; 0; 1) и D (1; 1; 2). Найдите:
а) координаты вектора 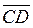 ; (2 балла)
; (2 балла)
б) абсолютную величину вектора 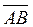 ; (2 балла)
; (2 балла)
в) координаты вектора 3·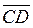 . (2 балла).
. (2 балла).
2. Найдите длину вектора 2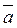 + 3
+ 3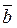 , если
, если 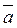 (1; 1;-1),
(1; 1;-1), 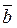 (2; 0; 0). (3 балла)
(2; 0; 0). (3 балла)
3. Найдите величину угла В треугольника АВС, если А (2; 2; -4), В(2; - 1; - 1), С(3; - 1; - 2). (3 балла)
Вариант 4
1. Дан вектор 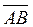 (1; - 1; 0) и точки C(1; 0; 2) и D(1; 1; 2). Найдите:
(1; - 1; 0) и точки C(1; 0; 2) и D(1; 1; 2). Найдите:
а) координаты вектора 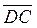 ; (2 балла)
; (2 балла)
б) абсолютную величину вектора 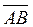 ; (2 балла)
; (2 балла)
в) координаты вектора 2·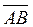 . (2 балла).
. (2 балла).
2. Векторы 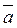 и
и 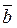 перпендикулярны, причем
перпендикулярны, причем 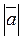 = 6,
= 6, 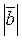 = 8. Найдите
= 8. Найдите 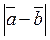 . (3 балла)
. (3 балла)
3. Найдите величину угла А треугольника АВС, если А(2;-2;-3), В(4;- 2;- 1), С(2; 2; 1). (3 балла)
Тематическое оценивание № 6 можно провести с помощью теста, текст которого представлен ниже.
При оценивании выполнения тестов учитываются только те шесть из выполненных заданий, которым соответствует наибольшее количество баллов.
Тест
Координаты и векторы в пространстве
Цель данного теста - проверить, умеет ли учащийся:
- изображать точку, заданную координатами, и выполнять обратную задачу;
- вычислять расстояние между двумя точками, заданными координатами; находить координаты середины отрезка;
- выполнять действия над векторами, заданными координатами;
- решать простые задачи на нахождение угла между прямой и плоскостью; между двумя скрещивающимися прямыми, между плоскостями.
Вариант 1
И уровень
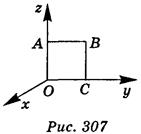
1. Сторона квадрата ОАВС, который лежит в плоскости zв, равна 1 (рис. 307). Найдите координаты точки В. (1 балл)
2. а) В(1; 1; 0); б) В(0; 1; 1); в) (1; 0; 1); г) (1; 1; 1).
3. Даны точки A(2;3;1), B(1;0;2). Найдите координаты вектора 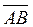 . (1 балл)
. (1 балл)
4. а) 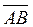 (3; 3; 3); б)
(3; 3; 3); б) 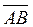 (1; 3; -1); в)
(1; 3; -1); в) 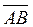 (-1; -3; 1); г)
(-1; -3; 1); г) 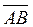 (-3; -3; -3).
(-3; -3; -3).
5. Дано изображение куба (рис. 308). Найдите угол между прямыми а и b. (1 балл)
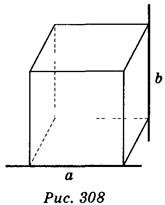
6. а) 45°; б) 0°; в) 90°; г) определить невозможно.
II уровень
1. Чему равно расстояние между точками А и В, если A(1;1;1), В(-1;-1;1)? (1 балл)
а)  ; б) 2
; б) 2 ; в) 2
; в) 2 ; г) 8.
; г) 8.
2. Какая из указанных точек С является серединой отрезка АВ, если А(1; 2; 3), В(3; 1; 1)? (1 балл)
a) C(1; 1; 1); б) С(2; 2; 2); в) С(-1; 0; 2); г) С(4; 4; 4).
3. При каких значениях п векторы 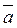 (1; -1; n) и
(1; -1; n) и 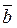 (n; 1; n) коллинеарны? (1 балл)
(n; 1; n) коллинеарны? (1 балл)
а) Ни при каких; б) при n = -1; в) при n = 1; г) при n = ±1.
III уровень
1. Найдите координаты вершины D параллелограмма ABCD, если А (0; 2; 0), В (1;0;0); С(2; 0; 2). (2 балла)
a) D(1;2;3); б) D(2;2;1); в) D(1;2;2); г) D(2;1;2).
2. Из одной точки к плоскости проведены равные наклонные. Угол между ними 60° , а между их проекциями - 90° . Найдите углы между наклонными и плоскостью. (2 балла)
а) 30°; б) 60°; в) 45°; г) 90°.
3. Две плоскости пересекаются под углом 60°. Точка М находится от этих плоскостей на расстоянии 4 см. Найдите расстояние от точки М до линии пересечения плоскостей. (2 балла)
а) 2 см; б) 4
см; б) 4 см; в) 4 см; г) 8 см.
см; в) 4 см; г) 8 см.
IV уровень
1. Дано точки А(2; 1; 7), В(-1; 1; 3), С(-8; 1; 2). Найдите внутренний угол В треугольника АВС. (3 балла)
а) 45°; б) 60°; в) 135°; г) 90°.
2. Даны точки А(1; 0; 0), B(0; 0; 1), C(0; 1; 1), D(1; 1; 0). Найдите площадь четырехугольника ABCD. (3 балла)
а) 1; б)  ; в) 2; г)
; в) 2; г)  .
.
3. Найдите тангенс угла между диагональю куба и плоскостью одной из его граней. (3 балла)
а)  ; б)
; б) 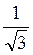 ; в)
; в)  ; г)
; г) 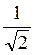 .
.
Вариант 2
И уровень
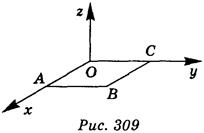
1. Сторона квадрата ОАBС, который. лежит в плоскости ху, равна 1 (рис. 309). Найдите координаты точки В.
(1 балл) а) В(0; 1; 1); б) B(1; 0; 1); в) B(1; 1; 0); г) B(1; 1; 1).
2. Каком из указанных векторов равна вектор 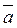 (1; 2; 3)? (1 балл)
(1; 2; 3)? (1 балл)
а) 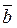 (2; 3; 1); б)
(2; 3; 1); б) 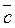 (3; 1; 2); в)
(3; 1; 2); в) 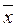 (1; 2; 3); г)
(1; 2; 3); г) 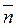 (1; 3; 2).
(1; 3; 2).
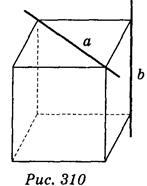
3. Дано изображение куба (рис. 310). Найдите угол между прямыми а и b. (1 балл)
а) 45°; б) 0°; в) 90°; г) определить невозможно.
II уровень
1. Найдите длину вектора 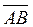 , если А (-1; 1; -1), B(1; -1; -1). (1 балл)
, если А (-1; 1; -1), B(1; -1; -1). (1 балл)
а)  ; б) 2
; б) 2 ; в) 2
; в) 2 ; г) 8.
; г) 8.
2. Точка C(1; 1; 1) является серединой отрезка АВ, причем B(1; 3; -1). Найдите координаты точки А. (1 балл)
а) А(0;0;0); б) А(1;0;3); в) А(1;-1;0); г) А(1;-1;3).
3. При каком значении n векторы 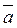 (2; 1; n) и
(2; 1; n) и 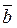 (n; 1; n) перпендикулярны? (1 балл)
(n; 1; n) перпендикулярны? (1 балл)
а) n = 1; б) n = -1; в) n = ± 1; г) ни при каких n.
III уровень
1. Найдите координаты вершины А параллелограмма ABCD, если B(1;0;1), C(1;1;0); D(1;1;1). (2 балла)
а) А(2; 1; 2); б) А 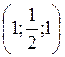 ; в) А(1; 0; 2); г) А(2; 0; 1).
; в) А(1; 0; 2); г) А(2; 0; 1).
2. Из одной точки к плоскости проведены две равные наклонные, образующие с перпендикуляром углы по 45°, а между собой - 60°. Найдите угол между проекциями наклонных на эту плоскость. (2 балла)
а) 30°; б) 60°; в) 45°; г) 90°.
3. Две плоскости пересекаются под углом 60°. Точка М находится на одинаковом расстоянии от этих плоскостей и на расстоянии 2 см до линии пересечения плоскостей. Найдите расстояние от точки М до этих плоскостей. (2 балла)
а) 2 см; б) 1 см; в) 0,5 см; г) определить невозможно.
IV уровень
1. Даны точки А(-1;-2;-1), В(-1;-1;0), С(-1; -1; -1). Найдите величину угла ВАС. (3 балла)
а) 135°; б) 60°; в) 90°; г) 45°.
2. Даны точки А(0; 2; 0), B(1; 0; 0), C(2; 0; 2), D (1; 2; 2). Найдите площадь четырехугольника ABCD. (3 балла)
а) 2; б) 2 ; в) 2
; в) 2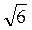 ; г) 2
; г) 2 .
.
3. Дан тетраэдр, все ребра которого равны. Найдите тангенс угла между боковым ребром и плоскостью основания тетраэдра. (3 балла)
a)  ; б)
; б)  ; в) 1; г) определить невозможно.
; в) 1; г) определить невозможно.
Ответы к тестовым заданиям
Уровень |
Номер задания |
Вариант 1 |
Вариант 2 |
И |
1 |
б |
в |
2 |
в |
в |
3 |
в |
в |
II |
1 |
б |
в |
2 |
б |
г |
3 |
а |
б |
III |
1 |
в |
в |
2 |
в |
г |
3 |
г |
б |
IV |
1 |
в |
г |
2 |
б |
в |
3 |
г |
б |
II. Домашнее задание
Если в классе выполнялась тематическая контрольная работа № 6, то дома можно предложить выполнить тест, и наоборот.
III. Подведение итога урока
В ходе фронтальной беседы выяснить, какие задания вызвали трудности, и ответить на вопросы учеников.








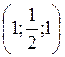 ; в) А(1; 0; 2); г) А(2; 0; 1).
; в) А(1; 0; 2); г) А(2; 0; 1).