ГЕОМЕТРИЯ

Раздел ІІ. СТЕРЕОМЕТРИЯ

§29. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ.

3. Условие перпендикулярности векторов, заданных координатами.

Поскольку 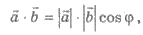где φ - угол между векторами, то имеем условие перпендикулярности векторов: если векторы перпендикулярны, то их скалярное произведение равно нулю, и наоборот: если скалярное произведение векторов равно нулю, то векторы перпендикулярны.

Если заданы координаты векторов 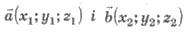, то условием перпендикулярности векторов является

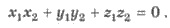
Пример 1. Или перпендикулярны векторы: 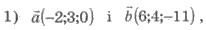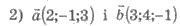перпендикулярные?

Решения. 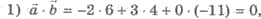поэтому .

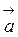
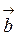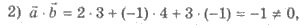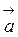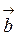поэтому векторы i не перпендикулярны.

Пример 2. При каком значении х векторы 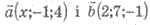перпендикулярны?

Решения. Чтобы векторы были перпендикулярны, то их скалярное произведение должно быть равно нулю: 2х - 7 - 4 = 0; 2х = 11; х = 5,5.