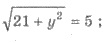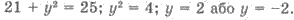ГЕОМЕТРИЯ

Раздел ІІ. СТЕРЕОМЕТРИЯ

§28. КООРДИНАТЫ ВЕКТОРА. ДЕЙСТВИЯ НАД ВЕКТОРАМИ, ЧТО ЗАДАНО КООРДИНАТАМИ.

Так же, как и на плоскости задаются координаты вектора в пространстве, только если на плоскости вектор задается двумя координатами, то в пространстве - тремя. Аналогично задаются также действия над векторами в пространстве, скалярное произведение векторов и т.д.

Советуем повторить §30 раздела И перед дальнейшим изучением этого параграфа.

1. Координаты вектора в пространстве. Равенство векторов, заданных координатами. Модуль вектора.

Если в пространстве ввести систему координат, то каждый вектор можно задать тройкой чисел - координатами вектора в просторные.

Координатами вектора 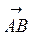с началом А(х₁; у₁; z₁) и концом В(х₂; у₂; z₂) называют числа х = х₂ - х₁; у = у₂ - у₁; z = z₂ - z₁.

Напомним, что записывают вектор 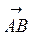, указывая его координаты следующим образом 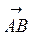(х;у;z). Например, 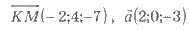т.д.

Пример 1. Найти координаты вектора 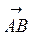, если А(-5; 2; -3), B(7; -1; 0).

Решения. 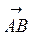(7 - (-5);-1 - 2;0 - (-3)) ,итак 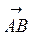(12;-3;3).

Координаты вектора могут быть любые действительные числа. Все координаты нулевого вектора равны нулю 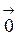(0;0;0).

Как и на плоскости,

равные векторы имеют соответственно равны координаты, и наоборот: если у векторов соответственно равны координаты, то векторы уровне.

Пример 2. Даны точки А(-1;3;4), В(0;5;-1), С(х;2;z), D(1;у;-2). Найти х, у, z, если = .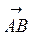

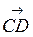Решения.

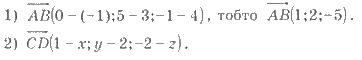
3) Поскольку 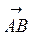= 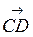, то имеем 1 - х = 1; у - 2 = 2; -2 - z = -5.

Итак, имеем х = 0; в = 4; z = 3.

Модуль вектора 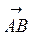(х;у;z) равна

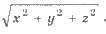
Пример 3. Найти модуль вектора: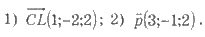

Решения.

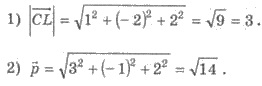
Пример 4. Известно, что модуль вектора 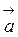(-4;у;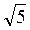) равна 5. Найти y.

Решения.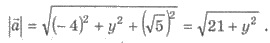

По условию