ГЕОМЕТРИЯ

Раздел ІІ. СТЕРЕОМЕТРИЯ

§18. УСЕЧЕННАЯ ПИРАМИДА.

1. Определение усеченной пирамиды. Элементы усеченной пирамиды.

Рассмотрим произвольную пирамиду QАВС...L. Проведем плоскость α, параллельную к основанию пирамиды. Эта плоскость пересекает боковые ребра пирамиды в точках А₁, В₁, С₁, ... ,L₁ (рис. 475). Плоскость α разбивает пирамиду на два многогранники.

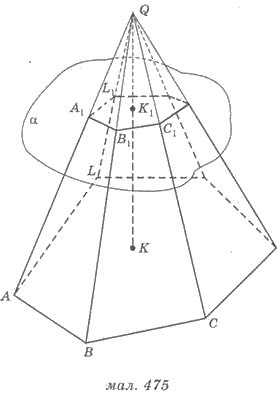
Многогранник, гранями которого являются многоугольники АВС...L и А₁В₁С₁...L₁ (нижнее и верхнее основания), расположенные в параллельных плоскостях и четырехугольники АА₁В₁В, BВ₁С₁C,...,LL₁А₁A (боковые грани) называют срезанной пирамидой. Отрезки АА₁, ВВ₁, СС₁, ...,LL₁ называют боковыми ребрами усеченной пирамиды.

Срезанную пирамиду с основами АВС...L и А₁В₁С₁...L₁ обозначают так АВС...LА₁В₁С₁...L₁.

Срезанную пирамиду называют n-угольной, если ее основами являются n-угольники.

Перпендикуляр, проведенный из некоторой точки одного основания к плоскости другого основания, называется высотой усеченной пирамиды. На рисунке 475 отрезок УК₁ - высота усеченной пирамиды.

Свойства усеченной пирамиды:

1) Боковыми гранями усеченной пирамиды есть трапеции.

2) Основания усеченной пирамиды - подобные многоугольники.