Урок
№ 5
Тема. Определение угла. Равенство углов. Биссектриса угла.
Измерения и откладывания углов
Цель: добиться от учащихся
усвоение содержания таких понятий: «угол», «элементы угла», «обозначение угла»,
«внутренняя область угла», «луч, делящей данный угол на два угла»,
«развернутый угол», «равные углы», «биссектриса угла и аксиомы измерения и
откладывание углов», «виды углов».
Сформировать умения:
·
воспроизводить
определение названных выше понятий и аксиом;
·
описывать,
опираясь на названные понятия, готовые рисунки и, наоборот, по данным описанием
делать соответствующий рисунок;
·
без
помощи измерительных инструментов определять вид угла по его градусной
мере).
Тип урока: усвоение знаний,
умений и навыков.
Форма проведения: фронтальная
практическая работа.
Наглядность i
оборудование: таблицы
«Отрезки», «Углы».
ХОД УРОКА
И. Организационный
момент
Учитель побуждает
учащихся к самопроверке готовности к уроку и сообщает тему и план работы на
уроке.
II.
Проверка домашнего задания
Самостоятельная
работа
Вариант 1
1. Точка N лежит
между точками M и K. MN = 8,4 см, KM =18,3 см. Найдите NK.
2. Дано AC = 9 см, CB = 4 см, BD =12 см. Найдите AB, CD, AD.
3. На прямой
отмечены точки A, B и C, причем AB = 24 см, BC =18 см. Найдите расстояние от точки A до середины отрезка BC. Сколько решений имеет задача?
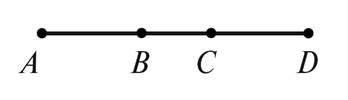
Вариант 2
1. Точка C лежит
между точками A и B. AB = 8,3 см, CB = 4,8 см. Найдите AC.
2. Дано LM = 15 см, NK = 16 см, MK = 24 см. Найдите MN, LK, NL.
3. На прямой
отмечены точки A, B и C, причем AB = 24 см, а расстояние от точки C до середины отрезка AB равна 17 см. Найдите длину отрезка AC. Сколько решений
имеет задача?
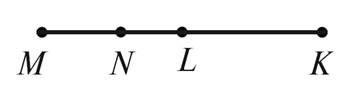
III.
Формулировка цели и задач урока. Мотивация учебной деятельности
Определенный мотивационный
момент произошел во время выполнения домашнего задания (задача 4). Ученики
получили толчок к размышлениям в направлении того, что два луча с одним началом
могут образовать как знакомую им фигуру - прямую, так еще не изученную фигуру - угол
(понятно, что эта фигура является также знакомой учащимся с 5 класса). Исходя из новых
условий изучения фигур, учитель вместе с учениками формулирует основную дидактическую цель
урока.
IV.
Актуализация опорных знаний
Перед формулировкой
определение угла, понятий равенства углов, биссектрисы угла и аксиом измерения и
откладывание углов уместно будет повторить аналогичные понятия, определения, аксиомы
относительно отрезков, обратившись при этом к таблице «Отрезки».
V.
Усвоение новых знаний
План изучения
нового материала
1°. Определение угла.
Элементы угла. Обозначения углов.
2°. Внутренняя область
угла. Луч, который делит угол на два угла.
3°. Развернутый угол и
его внутренняя область.
4°. Равенство углов.
Биссектриса угла.
5°. Измерение углов:
единицы измерения, аксиома измерения.
6°. Аксиома откладывания
углов сравнение углов по градусной мере.
7°. Виды углов.
Методический комментарий
Как понятие
отрезка, так и понятие угла на интуитивном уровне знакома учащимся еще с 5 класса.
Поэтому главная задача урока - дать достаточно строгие математические формулировки
перечисленных выше объектов, опираясь на знания учащихся и используя прием
аналогии. Организуем практическую работу учащихся, выводами каждого из этапов которой
i будут указаны в теме урока понятие.
Задача 1
а) Отметьте
произвольную точку O. Постройте два доповняльні лучи OA и OB.
б) Отметьте
произвольную точку C. Постройте два луча CM и CN, что не является доповняльними.
Сравните, что
общего в образованных в пунктах а) и б) геометрических фигурах?
Из каких геометрических
фигур состоят фигуры на рисунках?
Формулируем вывод
вместе с учениками (определение угла, его элементы и обозначения, внутренняя область
угла).
Задание 2
(Каждой паре учеников
раздаем набор пронумерованных бумажных моделей углов - различной градусной меры
и разные по размерам.)
Найдите и укажите
среди предложенных моделей углов: а) равные; б) неровные; в) наибольший; г)
наименьший.
Объясните, какие действия
выполняли при этом.
Формулируем выводы
вместе с учениками (определение равных углов, биссектрисы угла, возможно, свойства
углов, отложенных от одной пол прямой в одну півплощину).
Задание 3 (работа с теми самыми
бумажными моделями углов)
Каким еще отличным
от примененного в задании 2 способом можно проверить, есть ли среди углов: а)
уровне; б) наибольший; г) наименьший? Какой измерительный инструмент вы
применяли для этого в 5 классе? В каких единицах измеряли углы?
Вывод. (Формулируем содержание
понятие «измерение углов», «единицы измерения углов» и аксиомы измерения
i откладывания углов.)
Задание 4 (работа с моделями)
Сравнив градусные
меры углов, разделите их на четыре группы по градусной мере. Объясните свой выбор.
Вывод. (Рассматриваем виды
углов по градусной мере и свойство сравнение углов по градусной мере.)
После чего демонстрируем учащимся обобщенную
таблицу «Углы».
Таблица
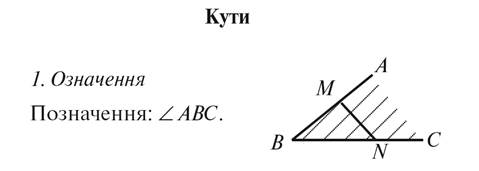


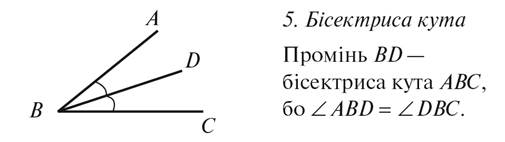

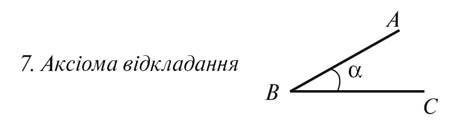
VI. Первичное
осознание нового материала
Выполнение
устных упражнений (по готовым рисункам)
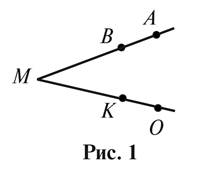
1. Можно угол,
изображенный на рисунке 1, обозначить так: AOM; AMO; AMB; OMA; MOA; AMK; OMK; ABO;
KMB; OKA?
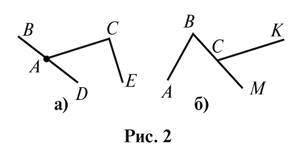
2. Назовите все углы,
что изображены на рисунке 2.
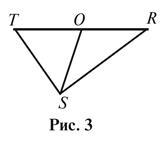
3. Назовите восемь
углов, изображенных на рисунке 3. Вместо чисел 1, 2, 3 выпишите такие с
названных углов, чтобы наверняка выполнялось равенство: 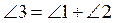 . Объясните свой выбор.
. Объясните свой выбор.
4. Как, имея только
лист бумаги прямоугольной формы, построить модель угла 180°; 90°; 45°? Покажите
это.
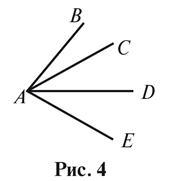
5. На рисунке 4:
а) назовите все углы;
б) назовите
наибольший угол;
в) найдите уровне
углы, если AC - биссектриса угла BAD и AD - биссектриса угла CAE.
VII.
Итоги урока
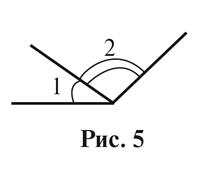
На рисунке 5 изображен
углы 1, 2. Могут выполняться равенства: 1) 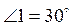 ,
, 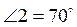 ; 2)
; 2) 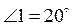 ,
, 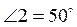 ; 3)
; 3) 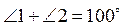 ? Ответ объясните.
? Ответ объясните.
VIII.
Домашнее задание
Выучить определения,
аксиомы, которые рассматривались на уроке.
Устно выполнить
упражнения.
1. Точки A, B и C не
лежат на одной прямой. Может угол ABC быть развернутым?
2. Определите, каким
(острым, прямым или развернутым) есть угол,который образуют стрелки часов в 3
часов; в 8 часов; в 11 часов; в 6 часов.
3. Назовите градусную
меру угла, на который поворачивается:
а) минутная стрелка
часов в течение 15 минут; 30 минут; 10 минут;
б) часовая стрелка
в течение 3 часов; 1 час; 30 минут.
4. Луч l делит
угол (mn) на два угла.
Сравните углы (ml)
i (mn).
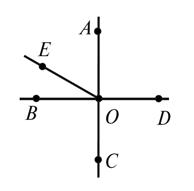
5.
На
рисунке назовите все острые углы; все прямые углы; все тупые углы.
6. Может ли сумма
градусных мер двух острых углов:
а) быть меньше
градусную меру прямого угла;
б) равняться
градусной мере прямого угла;
в) быть больше
градусную меру прямого угла;
г) быть больше
градусной мере развернутого угла?
7. Луч b - биссектриса
нераскрывшегося угла (ac). Может угол (ab) быть прямым; тупым?
Источники:
1. Уроки геометрии. 7 класс./ С. П. Бабенко
- Х.: Изд. группа «Основа», 2007.- 208 с.