|
III. Формулировка цели и задач урока С целью сознательного участия учащихся в формулировке цели урока можно провести беседу, во время которой предложить учащимся ответить на следующие вопросы: • Какие дроби называются обыкновенными? • Какие действия с обыкновенными дробями вы научились выполнять в 6 классе? • Какие дроби называются рациональными? Чем похожи рациональные дроби на обычные, а чем они отличаются? • Какие действия с рациональными дробями вы научились выполнять в 8 классе? • Похожие формулы, выражающие алгоритмы изученных действий с рациональными дробями, на соответствующие формулы для дробей? После окончания беседы ученики должны осознать цель урока: сформулировать и доказать правила сложения и вычитания рациональных дробей с одинаковыми знаменателями и сформулировать умение их применять на практике.
IV. Актуализация опорных знаний и умений @ С целью успешного овладения учениками учебным материалом урока перед его изучением следует активизировать знания и умения школьников по выполнению сокращение, сложение и вычитание дробей; преобразование целых выражений (сложение и вычитание многочленов, разложение многочленов на множители), а также сокращение рациональных дробей. Выполнение устных упражнений 1. Вычислите: 2. Представьте в виде произведения: 25 - y2; a2 + ab; 8 + x3; 1 + а2 - 2а; 3х6 - 12х2; b10 - b6. 3. Среди выражений найдите пары равных (для лишнего - составьте тождественно равное выражение): а) (х + у) - (а + b); б) х + у - а + b; в) х + y - a - b; г) х + у + а - b; д) (х + у) - (а - b).
V. Усвоение знаний План изучения нового материала 1. Правило сложения рациональных дробей с одинаковыми знаменателями и его доводки. Алгоритм выполнения сложения рациональных дробей с одинаковыми знаменателями. 2. Правило вычитания рациональных дробей с одинаковыми знаменателями и его доводки. Алгоритм выполнения вычитания рациональных дробей с одинаковыми знаменателями. 3. Примеры применения составленных алгоритмов.
@ Изучения материала урока начинается с формулировки правила сложения рациональных дробей с одинаковыми знаменателями в словесной форме и в виде тождества На основании доказанного правила далее составляется примерная схема действий (алгоритм) при добавлении рациональных дробей с одинаковыми знаменателями, причем, составляя алгоритм, желательно обращать внимание учащихся как на общие, так и отличительные черты алгоритмов сложения и вычитания обыкновенных и рациональных дробей. (Общее правило, отличное - выполняя действия сложения числителей этих дробей, следует пользоваться правилом сложения многочленов). После окончания изучения вопроса о сложении рациональных дробей с одинаковыми знаменателями следует рассмотреть примеры на применение составленного алгоритма. Изучение вопроса о вычитание рациональных дробей с одинаковыми знаменателями осуществляется по такой же схеме, как и сложения рациональных дробей (см. выше).поэтому, при условии высокого уровня интеллектуальной активности учащихся, этот фрагмент урока можно провести в форме самостоятельной работы по изучению нового материала по готовому плану.
VI. Усвоение умений Выполнение устных упражнений 1. Преобразуйте в дробь выражение: а) 2. Сократите дробь: а) 3. Найдите допустимые значения переменной в выражениях: х2 - 9; Выполнение письменных упражнений @ Для реализации дидактической цели на этом уроке следует решить задачи следующего содержания. 1. Сложение и вычитание рациональных дробей с одинаковыми знаменателями (на прямое применение алгоритмов). 1) Выполните сложение (вычитание) дробей: а) 2) Упростите выражение: а) 2. Преобразования суммы или разности рациональных дробей в рациональный несократимый дробь (на применение алгоритмов сложения и вычитания вместе с алгоритмом сокращение рациональных дробей). 1) Найдите значение выражения: а) 2) Упростите выражение: а) 3. Нахождение значения дробного выражения с предварительным упрощением его. Найдите значение выражения: а) 4. Выполнение упражнений на повторение: возведение дроби к новому знаменателю, нахождение ОДЗ рационального дроби, нахождение значений переменных, при которых рациональный дробь равна нулю. 1) Сократите дробь: а) 2) Сократите дробь: а) 3) Укажите область допустимых значений выражения: а) 5. Выполнение логических упражнений и заданий повышенного уровня сложности для учащихся, имеющих достаточный и высокий уровни знаний. 1) Упростите выражение: а) Указание: а) Многочлен х4 + х2 +1 можно разложить на множители, записав его в виде (х4 +2х2 + 1) - х2.
Упражнения, которые предлагаются для решения на этом уроке, должны способствовать формированию устойчивых навыков сложения и вычитания в простых случаях (при этом отрабатывается важный момент: правильная запись суммы и самое главное - разности числителей - полиномы представленных дробей в виде суммы или разности многочленов с последующим преобразованием записанного выражения в многочлен стандартного вида. Подготовительная работа проводится во время выполнения устных упражнений). После успешного разработка правил сложения и вычитания в простых случаях ученики могут постепенно переходить к совместного применения двух правил: правил сложения (вычитания) и сокращение дробей. В более сложной ситуации некоторые учащиеся могут допускать ошибки, что связано с сокращением дроби на слагаемое. Поэтому уже во время решения первых упражнений от учащихся следует требовать четкой последовательности действий: • преобразовать выражение в дробь; • если возможно, разложить на множители числитель и знаменатель; • выполнить сокращение, если в числителе и знаменателе дроби с общие множители.
VII. Итоги урока Правильно ли выполнены действия? Найдите и исправьте ошибку. а)
VIII. Домашнее задание 1. Изучить правила сложения и вычитания рациональных дробей с одинаковыми знаменателями (с доведением для сильных учеников). 2. Выполнить упражнения на применение изученных на уроке алгоритмов (уровень сложности задач соответствует уровню сложности задач классной работы). 3. На повторение: упражнения на применение правила знаков (тема «Основное свойство дроби»).
|
|
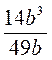 ; б)
; б) 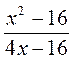 ; в)
; в) 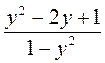 ; г)
; г) 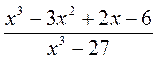 .
.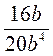 ; б)
; б) 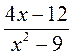 ; в)
; в) 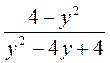 ; г)
; г) 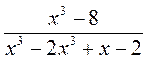
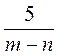 к знаменателю
к знаменателю 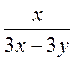 к знаменателю 3х2 - 6ху +3у2
к знаменателю 3х2 - 6ху +3у2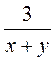 в знаменатель х2 - у2;
в знаменатель х2 - у2;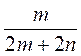 к знаменателю 2
к знаменателю 2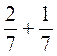 ;
; 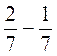 ;
; 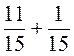 ;
; 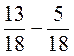 .
.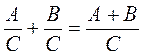
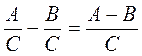
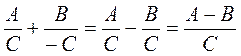
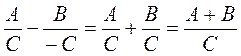
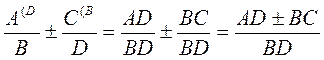
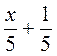 ; б)
; б) 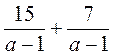 ; в)
; в) 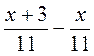 ; г)
; г) 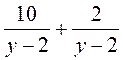 ; д)
; д) 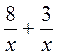 ; е)
; е) 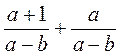 .
.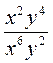 ; г)
; г) 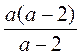 ; д)
; д) 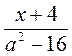 ; е)
; е) 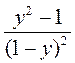 .
.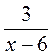 ;
; 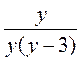 ;
; 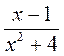 ;
; 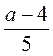 ;
; 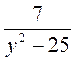 .
.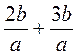 ; б)
; б) 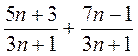 ; в)
; в) 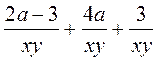 ; г)
; г) 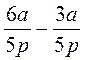 ; д)
; д) 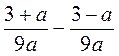 ; е)
; е) 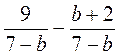 .
.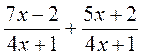 ; б)
; б) 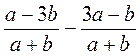 ; в)
; в) 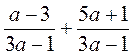 ; г)
; г) 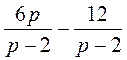 ; д)
; д) 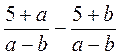 ; е)
; е) 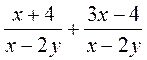 .
.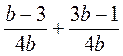 при
при 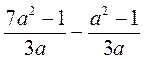 при а = 0,28.
при а = 0,28.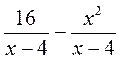 ; б)
; б) 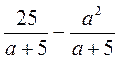 ; в)
; в) 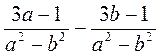 ; г)
; г) 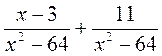 ; д)
; д) 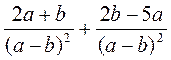 ; е)
; е) 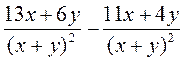 .
.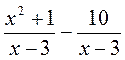 при х = 97; б)
при х = 97; б) 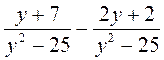 при у = -5,1.
при у = -5,1.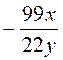 ; б)
; б) 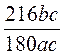 ; в)
; в) 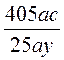 ; г)
; г) 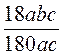 ; д)
; д) 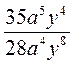 ; е)
; е) 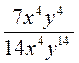 .
.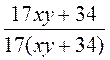 ; б)
; б) 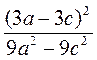 ; в)
; в) 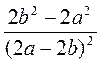 ; г)
; г) 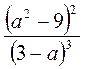 ; д)
; д) 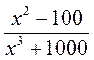 ; е)
; е) 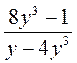 ; ж)
; ж) 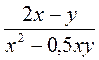 ; з)
; з) 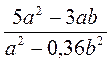 .
.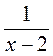 ; б)
; б) 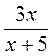 ; в)
; в) 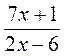 .
.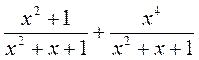 ; б)
; б) 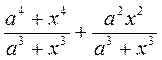 .
.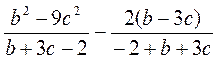
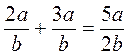 ; б)
; б) 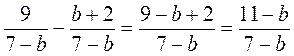 ; в)
; в) 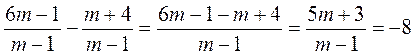 .
.