УРОК 5
Тема. Тригонометрические функции угла
Цель урока: повторить определение тригонометрических функций острого угла прямоугольного треугольника и ввести определение тригонометрической функции произвольного угла.
И. Анализ ошибок, допущенных в математическом диктанте и самостоятельной работе.
1. Постройте графики функций (индивидуальные карточки):
а) 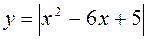 ; б)
; б) 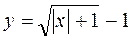 ; в)
; в) 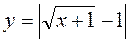 ; г)
; г) 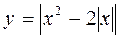 .
.
Ответ: а) рис. 25; б) рис. 26; в) рис. 27; г) рис. 28.
2. Постройте графики функций (индивидуальные карточки):
а) 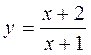 ; б)
; б) 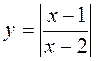
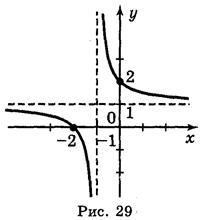
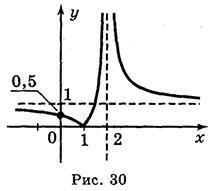
Ответ: а) рис. 29; б) рис. 30.
II. Повторение сведений о тригонометрические функции острых углов прямоугольного треугольника.
Провести повторение путем фронтальной беседы с использованием таблицы 3.

1. Дайте определение синуса острого угла прямоугольного треугольника.
2. Дайте определение косинуса острого угла прямоугольного треугольника.
3. Дайте определение тангенса острого угла прямоугольного треугольника. (Ввести понятие котангенса острого угла прямоугольного треугольника).
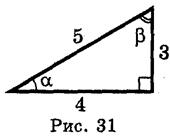
4. Пользуясь рис. 31 найдите sin α, cos α, tg α, ctg α, sin β, cos β, tg β, ctg β.

5. Вычислите:
а) 2 cos 60° +  cos 30°;
cos 30°;
б) 3tg45°·tg60°;
в) 2 cos 30° + 6 cos 60° - 4 tg 45°;
г) 2 ctg 60° - 2 sin 60°.
6. Упростите:
a) (1 - cosα)(1 + cosα);
6) tgα - ctgα + sin2 α + cos2 α.
III. Повторение сведений о тригонометрические функции произвольного угла
В курсе геометрии для углов от 0° до 180° было дано определение синуса, косинуса, тангенса с помощью круга. Напомним эти определения. Пусть дан круг радиуса R, центр которого находится в начале координат. Отложим от положительной полуоси в верхнюю півплощину угол α, вторая сторона которого пересечет окружность в точке Рα(х; у) (рис. 32).
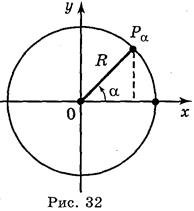
Синусом угла называется отношение ординаты точки Рα(х; у) окружности к ее радиусу: 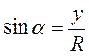 .
.
Косинусом угла называется отношение абсциссы точки Рα(.х; в) круга к его радиусу: 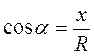 .
.
Тангенсом угла называется отношение ординаты точки Рα(х; у) к ее абсциссы: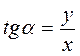 .
.
Котангенсом угла называется отношение абсциссы точки Рα(х; у) к ее ординаты: 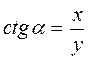 .
.
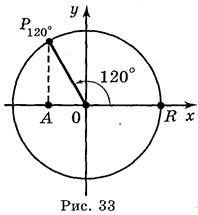
Пример 1. Найти sin α, cos α, tg α, ctg α, если α = 120°. Построив точку Р120º, имеем (рис. 33):
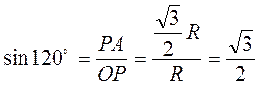 ;
; 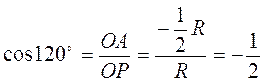 ;
; 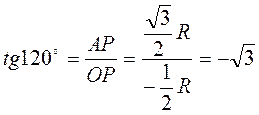 ;
; 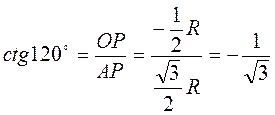 ;
;
Если любой угол рассматривать как фигуру, образованную вращением луча вокруг своей начальной точки в двух возможных направлениях (положительном - против часовой стрелки, отрицательном - по часовой стрелке), то данное определение можно использовать для любых углов.
Пример 2. Найти sin α, cos α, tg α, ctg α, если α = 270°. При повороте на 270° вокруг точки О радиус ОА, равный R, перейдет в радиус ОВ, тогда (рис. 34)
Р270º·(0; -R ) и, следовательно, sin 270° = 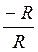 = -1, cos 270° =
= -1, cos 270° = 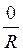 = 0, ctg270° =
= 0, ctg270° = 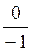 = 0 , tg 270° не имеет смысла.
= 0 , tg 270° не имеет смысла.
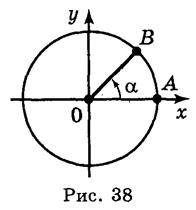
Из курса геометрии известно, что величина угла в градусах выражается числом от 0° до 180°. Угол Поворота может выражаться в градусах, каким угодно действительным числом от -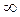 до +
до +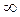 .
.
Пример 3. Если начальный радиус ОА сделал полный оборот против часовой стрелки, то угол поворота будет равен 360° (рис. 35). Если начальный радиус ОА сделал полтора оборота против часовой стрелки, то угол поворота будет равен 540º (рис. 36). Если начальный радиус ОА сделал два полных оборота и четверть оборота по часовой стрелке, то угол поворота будет равен 2 (-360°) - 90° = - 810° (рис. 37).
Рассмотрим радиусы ОА и ОВ. Существует множество углов поворота, при которых начальный радиус ОА переходит в радиус ОВ (рис. 38). Пусть AОВ = α, тогда соответствующие углы поворота будут равны α + 360°n, где n - целое число (n  Ζ).
Ζ).
Если начальный радиус переходит в радиус ОВ при повороте на угол а, то в зависимости от того, в какой четверти будет радиус 0B, угол α называют углом этой четверти. Так, если 0° α 90°, то α - угол i четверти; если 90° α 180°, то α - угол II четверти; если 180° α 270°, то α - угол III четверти; если 270° α 360°, то α - угол IV четверти. Углы 0°; ±90°; ±180°; ±270°; ±360° не относятся ни к какой четверти.
В курсе геометрии было доказано, что значения синуса, косинуса и тангенса угла α, где 0° α 180° зависит только от α и не зависит от длины R. И в общем виде sin α, cos α, tg α, а также ctg α зависят только от угла α.
Выражения sin α и cos α, определенные для любых а, так же как для любого угла поворота, можно найти отношением 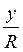 и
и 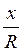 .
.
Выражение tg α имеет смысл при любых а, кроме углов поворота±90°; ±270°; ±450°, то есть α 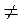 90°+180° n , (n
90°+180° n , (n  Ζ).
Ζ).
Выражение ctg α имеет смысл при любых а, кроме углов поворота 0°; ±180°; ±360°.., то есть, α 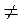 180° n, (n
180° n, (n  Ζ).
Ζ).
Каждому допустимому значению α соответствует единственное значение sin α, cos α, tg α, ctg α, поэтому синус, косинус, тангенс, котангенс являются функциями угла α. Их называют тригонометрическими функциями.
Выполнение упражнений
1. Чему равны углы поворота, которые показаны на рисунке 39.
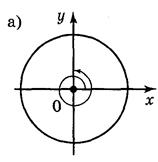
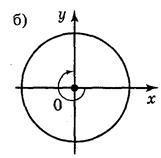
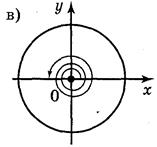
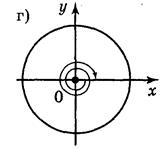
Рис. 39
2. Начертите круг с центром в начале координат и постройте угол поворота, равный: а) 135°; б) -120°; в) 540°; г) -810°.
3. Запишите все углы поворотов, при которых радиус ОА переходит в радиус ОВ (рис. 40).
4. Постройте окружность с центром в начале координат и углы поворота, которые равны:
а) 90° + 360° n, (n  Z);
Z);
б) 180° + 360° n, (n  Z);
Z);
в) -90º + 180° n, (n  Z);
Z);
г) ±60° + 360º n, (n  Z).
Z).
5. Определите, углом какой четверти является угол α, если угол а равен:
а) 181°; б) 179°; в) 271°; г) 361°; д) 345°; е) 800°.
6. Среди углов поворота 790°; 500°; -30°; 1580°; -220°; -290° найдите такие, при которых начальный радиус займет такое же положение, как и при повороте на угол: а) α = 70°; 6) α = 140°.
7. Начертите круг с центром в начале координат и радиусом R = 5 см. Верните начальный радиус на угол α и найдите приближенное значение sin α, cos α, tg α, ctg α, если α = 50°; 175°; -100°.
IV. Итог урока
V. Домашнее задание
Раздел И § 2. Вопросы и задания для повторения № 32-34. Упражнения № 4, 5.