ГЕОМЕТРИЯ

Раздел ІІ. СТЕРЕОМЕТРИЯ

§14. ПОНЯТИЕ СЕЧЕНИЯ МНОГОГРАННИКА.

При решении некоторых геометрических задач, связанных с многогранниками, полезно уметь строить на рисунке сечения многогранника различными плоскостями.

Будем называть секущей плоскостью многогранника любую плоскость, по обе стороны от которой имеются точки данного многогранника. Секущая плоскость пересекает грани многогранника по отрезках. Многогранник, сторонами которого являются эти отрезки, и называют сечением многогранника.

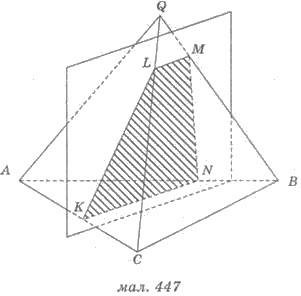
На рисунке 447 четырехугольник КLМN является сечением треугольной пирамиды QАВС.

Заметим, что в задачах секущую плоскость задают одним из знакомых нам способов:

1) тремя точками, не лежащими на одной прямой, или

2) прямой и точкой, не лежащей на ней, или

3) двумя прямыми, пересекающимися, или

4) двумя параллельными прямыми.

Для построения сечения достаточно построить точки пересечения секущей плоскости с ребрами многогранника, после чего провести отрезки, соединяющие каждые две построенные точки, принадлежащие одной и той же грани.

В дальнейшем будем рассматривать простейшие сечения призм и пирамид.