Часть 2 МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА

Раздел 5 ЯВЛЕНИЯ ПЕРЕНОСА

5.1. Число столкновений и средняя длина свободного пробега молекул. Эффективный диаметр молекулы

Средние скорости молекул газа очень большие - порядка сотен метров в секунду при обычных условиях. Например, за температуры 0 °С для молекул водорода, азота и кислорода величина равна соответственно 1700 м/с, 455 и 425 м/с. Однако процесс выравнивания неоднородности в газах вследствие молекулярного движения происходит слишком медленно, поскольку процессы диффузии и теплопроводности являются относительно медленными. Это можно объяснить так. Молекулы, перемещаясь, сталкиваются с другими молекулами. Газам умеренной плотности отвечает очень большое число столкновений за 1 с. При каждом столкновении скорость молекул изменяется по числовым значением и направлением. Между столкновениями молекулы движутся по прямым, а траектории их движения за некоторый промежуток времени Δτ является набором отрезков ломаной линии различной длины l₁, l₂, l₃,..., l_n (рис.5.1). Отрезки ломаной линии не лежат в одной плоскости. Поэтому если молекула вышла из точки А₁ и после n столкновений пришла в точку А₂, то эта конечная точка может лежать вблизи начальной точки, а расстояние между началом и концом траектории окажется значительно меньше, чем общий пройденный путь. Вследствие этого скорость, с которой молекула диффундирует из одной части газа в другую, значительно меньше средней скорости молекулярного движения.

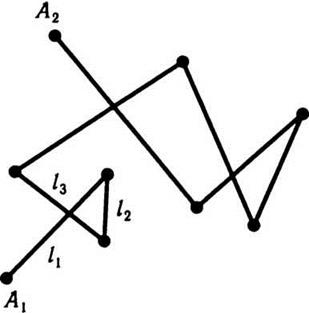
Рис. 5.1

Для оценки скорости движения молекул вводится понятие средней длины пути, который молекула проходит без столкновений (обозначается 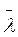). Для подсчета этого пути берут сумму длин отрезков траектории l₁, l₂, l₃,..., l_n от столкновения до столкновения и этот общий путь делят на количество отрезков п, равном количеству столкновений, т.е.

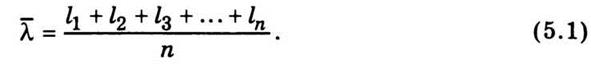
По этой формуле определяют средний путь, который молекула проходит свободно от столкновения до столкновения и который называется средней длиной свободного пробега молекул.

Для определения 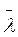определим сначала количество столкновений выбранной молекулы с другими молекулами за единицу времени.

Будем считать, что молекула после столкновения продолжает двигаться по прямой со средней скоростью движения . Молекулы, с которыми сталкивается выбранная молекула, в первом приближении считаем неподвижными и берем их сферические частицы радиуса r (рис. 5.2). Пусть выбранная молекула движется вправо из положения А₁ в положение А₂ по прямой O₁O₂. Во время движения она сталкивается с теми неподвижными молекулами, центры которых лежат не далее чем 2r от траектории движения O₁O₂ (например, молекула В с центром О). То есть молекула, которая движется со скоростью в течение 1 с, столкнется с теми молекулами, центры которых лежат внутри цилиндра с осью O₁O₂ и которые имеют радиус 2r и длину, равную . Действительно, за единицу времени молекула проходит расстояние, равное значению средней скорости движения молекул газа . Поэтому объем цилиндра, в котором содержатся заданные молекулы, будет 4πr².

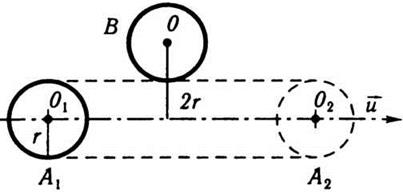
Рис. 5.2

Если концентрация молекул составляет n₀, то внутри заданного цилиндра содержится число молекул, равное z = 4πr²n₀. Это число z и определяет среднее количество столкновений за единицу времени. Поскольку другие молекулы находятся в движении, то в это число вводят поправочный множитель, равный 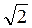. Поэтому среднюю количество столкновений за единицу времени определяют по формуле

Чтобы определить среднюю длину свободного пробега молекул, нужно путь, который проходит молекула за единицу времени (численно он равен ), поделить на количество соответствующих отрезков пути, то есть на среднее число столкновений z в единицу времен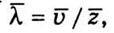и: или

Следовательно, средняя длина свободного пробега 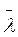не зависит от температуры газа, поскольку с повышением Т одновременно будет увеличиваться i .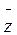

Значение средней длины свободного пробега используется, например, при описании диффузии, теплопроводности и других явлений.

При определении количества столкновений и средней длины свободного пробега молекул в первом приближении за модель молекулы взято упругую шарик.

На самом деле каждая молекула является сложной системой элементарных частиц, и во время рассмотрения упругого столкновения молекул принималось во внимание, что центры молекул могут сблизиться до некоторого наименьшего расстояния. После этого возникают силы отталкивания, которые вызывают взаимодействие, подобную до взаимодействия при упругом ударе. Среднее расстояние между центрами молекул, которые взаимодействуют так же, как при упругом ударе, называют эффективным диаметром.

Если в формулу (5.3) ввести эффективный диаметр σ = 2r, то получим следующее выражение:

Для оценки величины 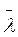, приведем такой пример. Для азота при нормальных условиях (давление 1 атм, температура 273 К) 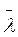≈ 0,6 ∙ 10^-7 м. Это примерно в 1000 раз больше от размеров молекул. Итак, время «взаимодействия» молекул во время столкновений во столько же раз (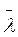/σ) меньше, чем время их свободного движения. Таким образом, столкновение даже при атмосферном давлении является довольно редким явлением.

Как видим из формулы (5.4), 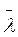~ 1 / г, поскольку Т = соnst, а г ~ n₀. При соответствующих значений р (сравнительно малых) значения 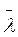могут сравниться с размерами сосуда, в котором хранится газ. Это означает, что газ находится в состоянии вакуума. Из формулы (5.4) следует, что 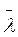молекул зависит также от их диаметра. Точные расчеты и эксперименты показывают, что определяющим при этом есть эффективный диаметр а, который зависит от температуры. По Г. Сезерлендом (1859-1912), эта зависимость описывается формулой

где σ₀ - истинный диаметр молекулы; С - стала Сезерленда. Значения С, определяемые из опытных данных по вязкости газов, показали, что С является не постоянной величиной, а некоторой функцией температуры. Для расчета С из экспериментальных данных уравнения Сезерленда применяют в такой форме:

где А = 2,7 ∙ 10^-21 - универсальная константа. Строя график зависимости Т^3/2/η от температуры, получим прямую, которая отсекает на оси температуры отрезок, равный С. Определенные таким образом значение С существенно зависят от ошибки в определении η. Так, ошибка в 1 % при определении η вызывает ошибку в определении С до 10 % . Величину С можно принять постоянной с некоторым приближением только для ограниченного интервала температур. В табл. 5.1 приведены значения для некоторых газов с указанием интервалов температур, в которых можно пользоваться этими значениями.

Таблица 5.1. Значение константы Сезерленда для различных газов

Была попытка установить аналитический выражение, который связывал бы константа Сезерленда с другими физическими константами. Установлено, что С пропорциональна критической температуре Т_к и связь с ею выражается соотношением С = Т_К /1,12, а также пропорциональная температуре кипения Т_ы при атмосферном давлении. Связь с с Т_s выражается соотношением С = 1,47 Т_s.

Хотя эти правила являются эмпирическими, они все же могут быть полезными для приближенных расчетов С.