ГЕОМЕТРИЯ
Раздел ІІ. СТЕРЕОМЕТРИЯ
§4. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ДВУХ ПЛОСКОСТЕЙ.
2. Параллельность плоскостей.
1. Две плоскости называют
параллельными, если они не имеют общих точек.
На рисунке 381 плоскости α и β
параллельные, это обозначают так: α || β.
Важной является признаки параллельности
плоскостей:
1. Если две прямые, которые
пересекаются, одной плоскости соответственно параллельны двум прямым другой плоскости,
то эти плоскости параллельны.
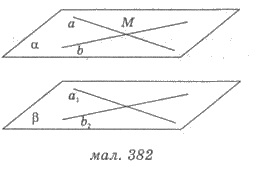
На рисунке 382: а
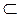 α; b
α; b 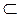 α;
α; 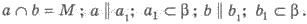 По признаку
параллельности плоскостей сделаем вывод о том, что α
|| β.
По признаку
параллельности плоскостей сделаем вывод о том, что α
|| β.
Следствие. Если две прямые, которые
пересекаются, одной плоскости параллельны другой, то плоскости параллельны.
2. Две плоскости, параллельные третьей,
параллельны между собой.
Также следует следующая теорема.
Через точку вне данной плоскости
можно провести плоскость, параллельную второй, и к тому же только одну.