Урок № 45

Тема. Разница квадратов. (Произведение разности двух выражений на их сумму)

Цель: (путем выполнения опережающего домашнего задания) индуктивным методом вывести формулу, известную как разность квадратов двух выражений, и таким образом добиться сознательного понимания учащимися содержания этой формулы; осуществить первичное закрепление формулы; выработать умение записывать, читать и применять формулу (a - b)(a + b) = a2 - b2 для преобразования выражений в многочлен стандартного вида.

Тип урока: усвоение знаний.

Ход урока

I. Организационный момент

@ Учитель побуждает учеников к проверке готовности к уроку, фиксирует фамилии отсутствующих.

II. Проверка домашнего задания

@ Одна из возможных форм проверки № 1 домашнего задания - организация самопроверки, когда ученики получают правильные решения в виде индивидуальных карточек-ксерокопий или как записи на доске (ксерокопии - лучший вариант, потому что экономим время) и самостоятельно сверяют свои решения с розданными. В случае необходимости ученики формулируют вопросы, ответы на которые дает учитель, либо ученики-консультанты (работу которых можно оценить).

III. Формулировка цели и задач урока

@ После проверки домашнего задания (№ 1 и № 2) учащимся напоминаем (или предлагаем осознать самим и сформулировать мысль), что, изучая тему «Многочлены», мы среди других, научились выполнять такое действие, как умножение двух многочленов. Причем на предыдущих двух уроках мы выяснили, что в некоторых отдельных случаях это действие можно выполнять «сокращенно» по соответствующим формулам сокращенного умножения. На уроке мы познакомимся еще с одной формулой, которую называют «разность квадратов».

IV. Работа с опережающим домашним заданием

@ Вопрос учащимся для самостоятельной проработки.

1. Что такое многочлен? члены многочлена? подобные члены многочлена?

2. Какой многочлен называют многочлен стандартного вида?

3. Как умножить одночлен на многочлен? многочлен на многочлен?

4. По алгоритму умножения двух многочленов выполнить умножение данных многочленов и свести образованные выражения в многочлен стандартного вида:

1) (x - y)(x + y); 2) (a - b)(a + b); 3) (c - d)(c + d); 4) (m - n)(m + n).

5. Прочитайте левую и правую часть образованных равенств, используя слова «произведение», «сумма», «разность». Сравните прочитанные выражения.

6. Сформулируйте выводы.

После проведения работы учащиеся презентуют свои ответы и корректируют выполненные задания. Цель этой работы: осознание факта, что произведение разности любых двух выражений на их сумму является разностью квадратов двух выражений.

V. Усвоение знаний

@ После выполненной работы с опережающим домашним заданием учителю остается лишь обобщить сформулированные умозаключения учащихся и составить соответствующий алгоритм. Очень важно (как и во время изучения других формул сокращенного умножения), чтобы ученики осознали, что в записи (a - b) (a + b) = a2 - b2 a и b - любые выражения (число, одночлен и даже многочлены) и знание формулы включает в первую очередь словесное ее формулировки.

В тетрадях учащиеся могут выполнить такую запись:

Выполнение устных упражнений

1. Прочитайте выражение:

(a + 8)2; а2 + 82; (0,2x - 4)2; (0,2x)2 - 42; x2 + 4; x2 - в2.

2. Возведите в квадрат выражение: 2; 2b; 2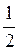b2; b2.

3. Укажите верное равенство:

1) (a - 2b)(a + 2b) = (a - 2b)2;

2) (a - 2b)(a + 2b) = a2 - 2b2;

3) (a - 2b)(a + 2b) = a2 + 4b2;

4) (a - 2b)(a + 2b) = a2 - 4b2.

Выполнение письменных упражнений

1. Представьте в виде многочлена выражение:

1) (х - у)(х + у);

2) (р + q)(р - q);

3) (b - а)(b + а);

4) (р - 7)(г + 7),

5) (2х - 1)(2х + 1);

6) (n - 3m)(3m + n);

7) (2а - 3b)(3b + 2а);

8) (10x - 7y)(10x + 7y).

2. Выполните умножение:

1) (х2 - 5)(х2 + 5);

2) (а2 + 3)(а2 - 3);

3) (а3 - b2)(а3 + b2);

4) (5х2 - 2у2)(5х2 + 2у2).

@ Во время выполнения этих упражнений важно требовать от учеников прочитать как условие, так и полученный результат (это обеспечивает более осознанное применение формулы). В работе с формулой на начальном этапе необходимо подчеркивать, что в формулировке записывается сначала разница (отрабатывая практические навыки, надо придерживаться принципа перехода от «простого к сложному», и этот переход нужно осуществлять постепенно, убедившись в сформированности навыков применения соотношение в более простой ситуации).

3. Представьте в виде многочлена:

1) 2(х - 3)(х + 3);

2) у(у + 4)(у - 4);

3) 5х(х + 2)(х - 2);

4)(3 - у)(3 + у)(9 + у2).

4. Упростите выражение:

1) 2х2 - (х + 1)(х - 1);

2) (3аb - 1)(3аb + 1) - 8а2b2;

3) (х - 2)(х + 2) - х(х + 5);

4) 2а(а + b) - (2а + b)(2а - b);

5) (3m - n)(3m + n) - (2m + n)(2m - n);

6) (5a - 3c)(5a + 3c) - (7c - a)(7c + a).

@ Если хватит времени, можно предложить упражнение на упрощение вычислений за счет применения формул.

5. Выполните вычисления:

1) (100 - 1)(100 + 1);

2) (80 + 3)(80 - 3); 3) 74 ∙ 66;

4) 201 ∙ 199;

5) 1002 ∙ 998;

6)1,05 ∙ 0,95.

VII. Итоги урока

Экспресс-контроль

1. Заполните пропуски в утверждении:

Произведение... двух выражений на их сумму... разницы... этих выражений.

2. Из записей правильный?

1) (х - 3у)(х + 3у) = х2 - 3у2; 2) (х - 3у)(х + 3у) = (х - 3у)2;

3) (х - 3у)(х + 3у) = х2 + 9у2; 4) (х - 3у)(х + 3у) = х2 - 9у2.

VIII. Домашнее задание

Используя формулу разности квадратов, выполните задания.

№ 1. Представьте выражение в виде многочлена:

1) (a + 5)(a - 5);

2) (4 + x)(4 - x);

3) (2a - 7)(2а + 7);

4) (12x + 13в)(12x - 13y);

5) (а3 - b4)(a3 + b4);

6) .

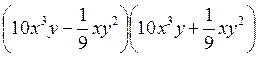№ 2. Упростите выражение:

1) (4х - 3у)(4х + 3у) + (3х + 4у)(4у - 3х);

2) (х + 2)2 - (х - 3)(х + 3);

3) (у - 2)(у + 3) - (у - 1)2 + (5 - у)(у + 5).

№ 3. Опережающее домашнее задание. По справочнику (5-6 класс) повторите:

1) закон умножения используется при умножении трех и более множителей?

2) Как изменится произведение двух выражений, если изменить знак одного множителя? обоих множителей?

3) Каким станет выражение, если изменить его знак на противоположный? (Как это сделать?) а; (а + b); (а - b), (-c - d + a); (-1 + d - a).
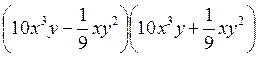