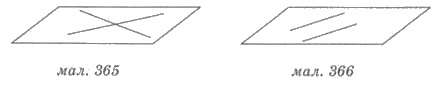ГЕОМЕТРИЯ

Раздел ІІ. СТЕРЕОМЕТРИЯ

§2. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМЫХ В ПРОСТРАНСТВЕ.

1. Прямые в пространстве.

Как известно из курса планиметрии, для двух прямых на плоскости возможны только два случая их взаимного расположения: или они пересекаются, или параллельны.

В пространстве возможен еще один случай размещение. Рассмотрим рисунок 364. Прямые АD/span> и D₁С₁ не имеют общих точек, кроме того они и не параллельны. В таком случае говорят, что две прямые не лежат в одной плоскости, то есть не существует такой плоскости, которая проходит через обе эти прямые.

Две прямые, которые не лежат в одной плоскости, называют скрещивающимися.

На рисунке 364 прямые АD и D₁С₁ - скрещивающиеся.

В планиметрии эти фигуры, которые мы рассматривали, размещались на одной плоскости. В стереометрии можно же рассматривать бесконечно много плоскостей. В связи с этим определение параллельных прямых требует уточнения.

Две прямые в пространстве называют параллельными, если они лежат в одной плоскости и не пересекаются.

Параллельность прямых а и b обозначают так же, как и в планиметрии: аllb.

Следовательно, в пространстве возможны три случая взаимного расположения двух прямых:

1) прямые лежат в одной плоскости и имеют общую точку - прямые, которые пересекаются (рис. 365).

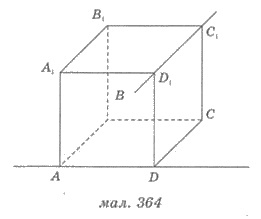
2) прямые лежат в одной плоскости и не имеют общих точек - параллельные прямые (рис. 366).

3) прямые не лежат в одной плоскости - скрещивающиеся прямые.