УРОК 35
Тема. Сравнение радикалов
Цель урока. Формирование умений учащихся сравнивать радикалы.
И. Проверка домашнего задания
1. Фронтальная беседа по № 25-37 из «Вопросы и задания для повторения» раздела III.
2. Самостоятельная работа.
Вариант 1
1. Найдите область определения выражения: а) 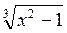 ; б)
; б) 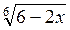 . (3 балла)
. (3 балла)
2. Вычислите: а) 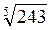 ; б) 5
; б) 5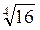 ; в)
; в) 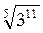 ·
·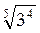 . (3 балла)
. (3 балла)
3. Упростите: а) 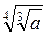 ; б)
; б) 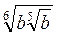 , b > 0. (3 балла)
, b > 0. (3 балла)
4. Или подобные радикалы 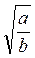 и
и 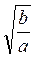 ? (3 балла)
? (3 балла)
Вариант 2
1. Найдите область определения выражения: а) 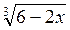 ; б)
; б) 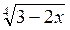 . (3 балла)
. (3 балла)
2. Вычислите: а) 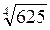 ; б) 4
; б) 4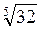 ; в)
; в) 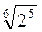 ·
·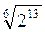 . (3 балла)
. (3 балла)
3. Упростите: а) 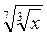 ; б)
; б) 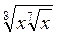 , х > 0. (3 балла)
, х > 0. (3 балла)
4. Или подобные радикалы 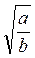 и
и 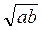 ? (3 балла)
? (3 балла)
Ответ:
В-1: 1. а) R; б) x 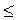 3. 2. а) 3; б) 10; в) 27. 3. а)
3. 2. а) 3; б) 10; в) 27. 3. а) 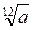 ; б)
; б) 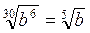 . 4. Подобные.
. 4. Подобные.
В-2: 1. а) R; б) х 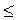 1,5. 2. а) 5; б) 8; в) 8. 3. а)
1,5. 2. а) 5; б) 8; в) 8. 3. а) 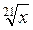 ; б)
; б) 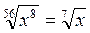 . 4. Подобные.
. 4. Подобные.
II. Восприятия и осознания материала о сравнения радикалов
Для сравнения радикалов применяется теорема:
Теорема: Если а > b  0, то
0, то 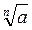 >
> 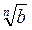 , то есть большем положительном підкореневому выражения соответствует и большее значение корня.
, то есть большем положительном підкореневому выражения соответствует и большее значение корня.
Доведение
Проведем доказательство методом от противного. Допустим, 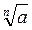
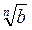 . Тогда по свойству степеней с натуральным показателем имеем
. Тогда по свойству степеней с натуральным показателем имеем 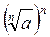
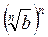 , т.е. а b. А это противоречит условию а > b.
, т.е. а b. А это противоречит условию а > b.
Пример. Сравним числа 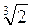 и
и 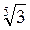 .
.
Представим 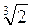 и
и 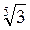 в виде корней с одним и тем же показателем:
в виде корней с одним и тем же показателем:
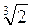 =
= 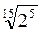 =
= 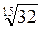 , а
, а 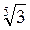 =
= 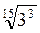 =
= 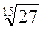 . Согласно доказанной теореме, так как 32 > 27, то
. Согласно доказанной теореме, так как 32 > 27, то 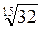 >
> 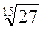 , а следовательно,
, а следовательно, 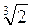 >
> 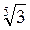 .
.
Выполнение упражнений
1. Сравните числа: а) 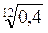 и
и 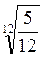 ; б)
; б) 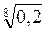 и
и 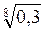 ; в)
; в) 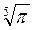 и
и 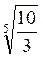 ; г)
; г) 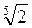 и
и 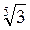 .
.
Ответ: а) 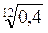
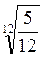 ; б)
; б) 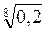
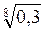 ;)
;) 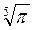
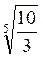 ; г)
; г) 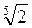
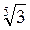 .
.
2. Что больше: а) 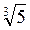 или
или 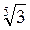 ; б)
; б) 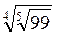 или
или 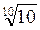 ; в)
; в) 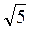 или
или 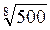 г)
г) 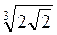 или
или 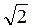 ?
?
Ответ: а) 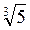 ; б)
; б) 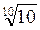 ; в)
; в) 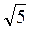 ; г)
; г) 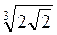 =
= 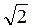 ?
?
3. Что меньше: а) 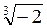 или
или 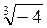 ; б)
; б) 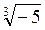 ли
ли 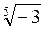 ?
?
Ответ: а) 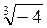 ; б)
; б) 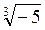 .
.
Непосредственно из доказанной теоремы следует:
1) Если а > 1, то 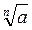 > 1 и
> 1 и 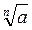 а.
а.
2) Если 0 а 1, то 0 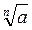 1 и
1 и 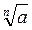 > а.
> а.
3) 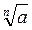 +
+ 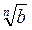 >
> 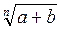 , при условии а > b
, при условии а > b  0 или b >
0 или b >  0.
0.
Выполнение упражнений
1. Определите знак выражения: а) 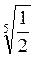 - 1 ; б)
- 1 ; б) 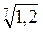 - 1; в)
- 1; в) 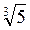 - 5; г)
- 5; г) 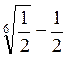 .
.
Ответ: а) - ; б) + ; в) - ; г) +.
2. Расположите в порядке возрастания: а)  ;
; 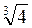 ;
; 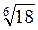 ; б)
; б) 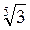 ;
; 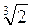 ;
; 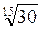 ;)
;) 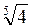 ;
; 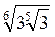 ;
; 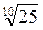 .
.
III. Подведение итогов урока
IV. Домашнее задание
Вопросы и задания для повторения раздела III № 13-15, 47. Упражнения № 22, 26, 38.