ГЕОМЕТРИЯ
Раздел И. ПЛАНИМЕТРИЯ
§1. ПРОСТЕЙШИЕ ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ НА ПЛОСКОСТИ И ИХ СВОЙСТВА.
1. Точка и прямая.
Геометрия - это наука о свойствах
геометрических фигур.
Планиметрия - часть геометрии, которая
изучает свойства геометрических фигур на плоскости.
Плоскость является одной из основных
геометрических фигур. Представление о части плоскости дает поверхность стола, стекла,
потолки и т.д. Плоскость и геометрии считают равной и неограниченной; она не имеет
края и не имеет толщины.
Основными геометрическими фигурами на
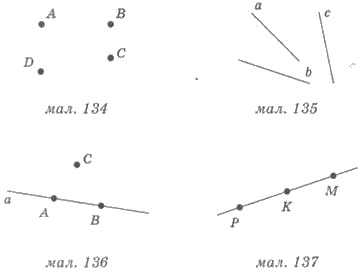
плоскости являются точка и прямая. Точки обозначают большими латинскими буквами А, В, С,
D... (илл. 134). Прямые можно проводить
с помощью линейки (рис. 135). При этом изображают часть прямой, а всю
прямую представляем бесконечной в обе стороны. Прямые зачастую обозначают малыми
латинскими буквами а, b, с.
На рисунке 136 изображен прямую а и
точки А, В, С. Точки А и В лежат на прямой а; говорят также, что точки А и В
принадлежат прямой а, или, что прямая а проходит через точки А и В. Точка С не
лежит на прямой а, иначе говоря, точка С не принадлежит прямой а, или прямая а не
проходит через точку С.
Какова бы не была прямая, существуют точки,
принадлежащие этой прямой, и точки, не принадлежащие ей.
Для удобства вместо слов «точка А
принадлежит прямой а» пользуются записью А 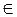 а , а вместо слов «точка С не принадлежит
прямой а» - записью С
а , а вместо слов «точка С не принадлежит
прямой а» - записью С 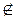 а.
а.
Заметим, что через точки А и В не
можно провести другую прямую, которая не совпадает с прямой а.
Через любые две точки можно
провести прямую, и только одну.
Прямую, на которой обозначены две точки,
например, А и В, можно заменить двумя буквами: АВ или ВА.
На рисунке 136 точка С не принадлежит
прямой АВ, это записывают так С 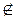 АВ. Говорят также, что точки А, В и С не
лежат на одной прямой.
АВ. Говорят также, что точки А, В и С не
лежат на одной прямой.
На рисунке 137 точки Р, К и М лежат
на одной прямой, причем точка К лежит между точками Г и Г.
Из трех точек на прямой одна и
только одна, лежит между двумя другими.