АЛГЕБРА И НАЧАЛА АНАЛИЗА

Раздел IV. ЭЛЕМЕНТЫ КОМБИНАТОРИКИ, НАЧАЛА ТЕОРИИ ВЕРОЯТНОСТЕЙ И ЭЛЕМЕНТЫ СТАТИСТИКИ

§3. ЭЛЕМЕНТЫ СТАТИСТИКИ.

3. Выборочные характеристики.

При статистических исследованиях выборки важным этапом является оценка ее числовых характеристик, которые называют выборочными характеристиками.

Размах выборки R - это разность между наибольшим и наименьшим значением случайной величины в выборке.

Для выборки, рассмотренной в примере 1 предыдущего пункта, должны R = 12 - 1 = 11.

Мода выборки М_O - то значение случайной величины, что встречается в выборке наиболее часто.

Для выборки, рассмотренной в примере 1 предыдущего пункта есть две моды - это числа 7 и 8. Можно записать М_O1 = 7; М_O2 = 8.

Медиана выборки М_е - срединное значение ранжованої выборки.

Медиана делит выборку на ранжовану две равные по количеству части. Если в выборке нечетное количество случайных величин, то его медианой является число, которое стоит посередине.

Например, в ранжированной выборке:

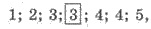
что состоит из 7 случайных величин, медианой является число 3. Можно записать М_е = 3.

Если в выборке четное число случайных величин, то медиана - среднее арифметическое двух чисел, стоящих посредине.

Например, в ранжированной выборке:

что состоит из 8 случайных величин, медиана - это среднее арифметическое чисел 4 и 5, что стоят посередине ряда. Следовательно, М_е = (4 + 5)/2.

Среднее арифметическое выборки 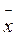- это среднее арифметическое всех ее значений x₁; x₂; x₃;...; x_n.

Так, например, среднее арифметическое выборки, рассмотренной в примере 1 предыдущего пункта находится следующим образом: