АЛГЕБРА И НАЧАЛА АНАЛИЗА

Раздел IV. ЭЛЕМЕНТЫ КОМБИНАТОРИКИ, НАЧАЛА ТЕОРИИ ВЕРОЯТНОСТЕЙ И ЭЛЕМЕНТЫ СТАТИСТИКИ

§2. ВЕРОЯТНОСТЬ СЛУЧАЙНОГО СОБЫТИЯ.

4. Решение задач на подсчет вероятностей с помощью формул комбинаторики.

Часто в задачах на подсчет вероятностей используют формулы комбинаторики. Рассмотрим примеры.

Пример 1. На карточках записаны натуральные числа: от 1 до 15. Наугад выбирают две из них. Какова вероятность того, что сумма чисел, записанных на этих карточках равна 10?

Решения. Количество всех возможных случаев - это количество способов, которыми можно (без учета порядка) выбрать две карточки с пятнадцати. Следовательно, n = С²₁₅ = 105. Нас устраивают такие наборы (1;9), (2;8), (3;7), (4;6). Следовательно,

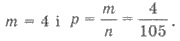
Пример 2. В ящике 7 белых и 3 черных шарики. Наугад выбирают три из них. Какова вероятность того, что 1) все они белые; 2) две из них - белые, а одна - черная?

Решения. Для обеих задач n = С³₁₀ = 120 - количество всех возможных случаев.

1) Выбрать три белые шарики можно С³₇ способами. Следовательно m = С³₇ = 35;

2) Выбрать две белые шарики можно С²₇ способами и после каждого такого выбора выбрать черную шарик можно С¹₃ способами. По правилу произведения