АЛГЕБРА И НАЧАЛА АНАЛИЗА

Раздел IV. ЭЛЕМЕНТЫ КОМБИНАТОРИКИ, НАЧАЛА ТЕОРИИ ВЕРОЯТНОСТЕЙ И ЭЛЕМЕНТЫ СТАТИСТИКИ

§2. ВЕРОЯТНОСТЬ СЛУЧАЙНОГО СОБЫТИЯ.

3. Классическое определение вероятности случайного события.

Случай, в результате которого происходит событие А, называют случаем, что способствует появлению события А.

Классическое определение вероятности случайного события состоит в следующем:

вероятность случайного события А равна отношению числа случаев m, благоприятствующих появлению события А, к числу всех возможных случаев n:

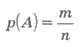
Заметим, что вероятность достоверной события р(U)= 1, а вероятность невозможной события г(V) = 0.

Рассмотрим примеры.

Пример 1. В урне 4 белых и 12 черных шариков. Наугад вынимаем одну с них. Какова вероятность того, что она белая (событие А)?

Решения. Из урны можно извлечь из равной вероятностью любую из 4 + 12 = 16 шариков. Поэтому n = 16. Число случаев, благоприятствующих появлению события А равна 4, т.е. m = 4. Следовательно, p(a) = 4/16 = 0,25.

Пример 2. На карточках написаны натуральные числа от 1 до 18. Наудачу извлекают одну из карточек. Какова вероятность того, что число, записанное на карточке, является делителем числа 18 (событие А)?

Решения. Понятно, что n = 18. Натуральными делителями числа 18 являются числа 1; 2; 3; 6; 9; 18. Следовательно, m = 6. Тогда р(А) = 6/18 = 1/3.

Пример 3. Одновременно подбросили два игральные кубики. Какова вероятность того, что сумма очков, выпавших на кубиках: 1) равна 7; 2) больше 8?

Решения. Составим таблицу суммы очков, которое может выпасть на двух игральных кубиках при их одновременном подбрасывании, n = 36 - число всех возможных случаев.

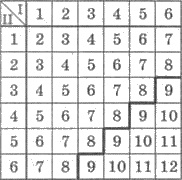
1) Есть 6 случаев, когда сумма очков на кубиках равна 7. Следовательно, m = 6. Тогда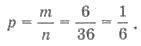

2) Есть 10 случаев, когда сумма очков на кубиках больше 8. Поэтому,