Часть 1 МЕХАНИКА

Глава 2 ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ

2.21. Звук. Эффект Доплера

Звук - это волновой процесс. В твердых телах звук распространяется в виде продольных и поперечных волн. Поскольку жидкости и газы практически не имеют упругости сдвига, то в таких средах звук распространяется только в виде продольных волн. В газах и жидкостях звуковые волны являются периодическими сгущениями и розрідженнями среды, удаляются от источника звука с определенной характерной для этой среды скоростью.

Звук характеризуется интенсивностью (силой) и составом и частотой связанных с ним волновых процессов. По по субъективным ощущениям различают следующие характеристики звука: громкость, тембр и высоту.

Собственно звуковыми колебаниями (звуком) называют колебания, распространяющиеся в упругой среде и частота которых лежит в пределах 16...20 000 Гц. Упругие волны с частотой меньше 16 Гц, называют інфразвуковими, а больше 20 000 Гц - ультразвукоными. Ультразвуковые колебания широко применяются в технике. В последнее время при изучении вещества интенсивно используют гіперзвук, которому соответствует частота свыше 10⁹ Гц.

Скорость распространения звука в воздухе при комнатной температуре равна 340 м/с. В воде звук распространяется со скоростью 1450 м/с, в стекле - 5600 м/с.

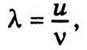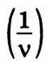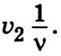Рассмотрим явление Доплера для звука. Пусть источник звука движется к наблюдателю со скоростью υ₂. Скорость звука обозначим через u, а частоту - через ν. Длина звуковой волны в случае неподвижного источника но при движении источника со скоростью υ₂ за один период длина волны уменьшится на Тогда длина звуковой волны, которую зафиксирует наблюдатель,

Следовательно, наблюдатель будет воспринимать звук меньшей длины волны λ'. При этом частота воспринимаемых колебаний увеличится и составит

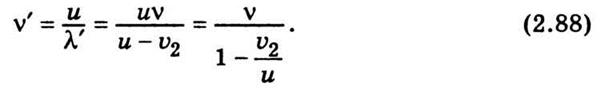
Нетрудно убедиться, когда источник звука будет удаляться от наблюдателя, частота воспринятого им звука будет

Если до неподвижного источника приближаться наблюдатель со скоростью υ₁, то при более частых «встречах» с гребнями волн частота воспринимаемых колебаний увеличится:

Так 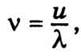то

При движении наблюдателя от недвижимого источники соответственно получим

В общем случае, когда одновременно движутся источник и наблюдатель, связь частоты воспринятого звука ν' и частоты звука источника ν выражаться объединенной формуле

где u - скорость звука; υ₁ - скорость движения наблюдателя; υ₂ - скорость источника звука относительно неподвижной системы координат.

Следовательно, на основании выражения (2.93) можно сделать такой вывод: уменьшение расстояния между источником звука и наблюдателем всегда сопровождается увеличением частоты воспринятого звука, и наоборот, увеличение расстояния между источником звука и наблюдателем приводит к уменьшение частоты воспринятого звука.