КИНЕМАТИКА

Урок № 3

Тема. Прямолинейное равномерное движение. Путь и перемещение. Скорость движения. Графики движения

Цель: усовершенствовать знания учащихся об равномерное прямолинейное движение; сформировать знания о скорости как векторную физическую величину, которая характеризует темп изменения перемещения; вырабатывать умение находить проекцию скорости и решать основную задачу механики для такого движения.

Тип урока: урок изучения нового учебного материала.

Наглядный: демонстрация равномерного прямолинейного движения, ППС «Физика-9» от «Квазар-Микро».

Ожидаемые результаты. После урока учащиеся:

- будут знать вид механического движения за его уравнением скорости;

- будут уметь находить проекцию скорости, решать основную задачу механики для прямолинейного равномерного движения, строить графики равномерного движения.

ХОД УРОКА

I. Проверка домашнего задания

• Обзор тетрадей с целью выяснения наличия решения учащимися задач, которые задали на дом.

• Физический диктант с взаимопроверкой.

II. Актуализация опорных знаний

Опыт. Демонстрация равномерного прямолинейного движения любого тела с записывающим устройством.

Ученики с повторенного материала за 8-й класс вспоминают характерный признак такого движения, формулу скорости, единицы скорости, формулу пути.

III. Мотивация, сообщение темы и цели урока

Новый материал следует рассмотреть с позиций решения основной задачи механики - научиться находить перемещения.

Прямолинейным равномерным движением называется движение, при котором материальная точка, двигаясь по прямой, за любые равные промежутки времени совершает одинаковые перемещения. Это простейший вид механического движения. Примером такого движения приближенно можно считать движение на прямолинейном участке ленты транспортера, ступеней эскалатора, движение поезда в метро после разгона, движение парашютиста и т.д.

Кинематическими характеристиками этого движения являются: перемещение, скорость, координата, путь. Во время прямолинейного движения только в одном направлении путь и длина вектора перемещения совпадают. Во всех других случаях модуль перемещения меньше длину пути, что с течением времени всегда растет.

Скоростью равномерного прямолинейного движения называют векторную физическую величину 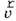, равную отношению вектора перемещения 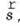к промежутку времени, в течение которого это перемещение произошло:

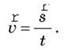
Направление вектора скорости в прямолинейном движении совпадает с направлением вектора перемещения. В равномерном прямолинейном движении за любые равные промежутки времени тело выполняет одинаковые перемещения, поэтому скорость такого движения является величиной постоянной.

Единица скорости в СИ - 1 м/с ; 1 м/с - это скорость такого равномерного прямолинейного движения, при котором материальная точка за 1 с совершает перемещение 1 м.

Пусть ось Ох системы координат, связанной с телом отсчета, совпадает с прямой, вдоль которой движется тело, а х0 является координатой начального положения тела. Вдоль оси Ox направленные и перемещение 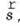, и скорость 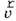движущегося тела (рис. 1).

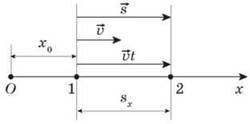
Рис. 1

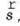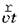Векторы и одинаковые, поэтому одинаковыми будут и их проекции на ось Ox:

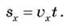
Кинематический закон равномерного прямолинейного движения, т.е. выражение для координаты движущегося тела в любой момент времени имеет вид:

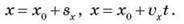
Это выражение называют уравнением равномерного прямолинейного движения. С его помощью, зная начальную координату х0 положение 1 (рис. 1) тела и его скорость в любой момент времени, можно определить положение движущегося тела. Правая часть этой формулы - алгебраическая сумма, поскольку х0 и x могут быть положительными и отрицательными. Знак плюс соответствует движению в положительном направлении оси Ox, знак минус - в отрицательном.

Если тело равномерно движется по прямой линии в плоскости, то это движение описывается системой уравнений:

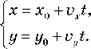
Во время прямолинейного равномерного движения в пространстве система примет вид:

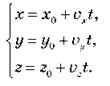
Во время прямолинейного движения вдоль координатной оси Ox путь равен изменению значений конечной и начальной координат, то есть s = x2 - x1, поэтому модуль скорости 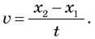Следовательно, скорость прямолинейного равномерного движения численно равна изменению координаты за единицу времени. Она показывает, как быстро изменяется координата x положения материальной точки.

Уравнение пути прямолинейного равномерного движения:

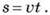
Путь, пройденный материальной точкой в случае прямолинейного равномерного движения, прямо пропорционален времени движения и всегда увеличивается.

Функциональную зависимость между кинематическими величинами можно выражать не только в виде уравнений, но и графически. Как пример рассмотрим график пути равномерного движения (рис. 2). Используем прямоугольную систему числовых осей, откладывая по оси абсцисс время, а по оси ординат - путь. График строят на основании уравнения s = t. Независимой переменной t предоставляют произвольных значений и определяют соответствующие значения s. Для равномерного движения со скоростью = 0,5 м/c - получают значения, приведенные в таблице:

После этого выбирают нужный масштаб, и значение каждой пары t и s из таблицы наносят на соответствующие числовые оси. В полученных точках ставят перпендикуляры до числовых осей. На пересечении соответствующих перпендикуляров отмечают точки O, A1, A2, A3, A4 и A5, через которые проводят линию, что является графику пути равномерного прямолинейного движения. Следовательно, график пути - прямая линия. Чем больше скорость, тем большим будет угол а между графиком пути и осью времени. Соответствующие масштабы по осям для каждого из сравниваемых графиков берутся одинаковыми.

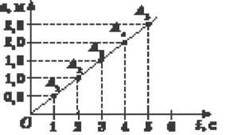
Рис. 2

Для построения графика скорости прямолинейного равномерного движения по оси ординат откладывают скорость, а по оси абсцисс - время. Поскольку во время равномерного движения скорость не меняется, то график скорости является прямой, параллельной оси времени. На рис. С показан график скорости прямолинейного равномерного движения ( = 2 м/c). С помощью графика скорости можно определить путь, пройденный телом за любой промежуток времени. Как видно из рис. 3, путь численно равен площади прямоугольника, одна сторона которого равна скорости, а вторая - заданном промежутке времени.

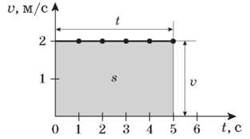
Рис. 3

Пусть два тела движутся равномерно вдоль оси Ox, одно - со скоростью 1 в положительном направлении оси, второй - со скоростью 2 в отрицательном направлении той же оси. Тогда x1 > 0, x2 0. На рис. 4 для этих тел изображены графики зависимостей проекций скоростей от времени. Эти графики параллельны оси времени t; второе тело движется с большей по модулю скоростью и в противоположном направлении.

Рис. 4

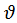На рис. 5 показаны графики зависимостей координат этих тел от времени, то есть графики зависимостей вида х, = x01 + x1t, х2 = х02 + x2t. Из графиков видно, что х01 > 0, х01 = х02, x1 > x2.

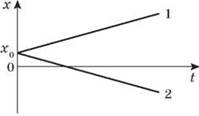
Рис. 5

Ученики анализируют по учебнику решения задач, делают записи в тетрадях.

IV. Обобщение и закрепление изученного материала

1. Фронтальное опрос

• Какое движение называют равномерным?

• Какой вид имеет выражение для координаты движущегося тела в любой момент?

• Графики зависимостей координат двух тел от времени являются параллельными. Охарактеризуйте скорости движения этих тел.

• Графики зависимостей перемещения двух тел от времени пересекаются. Обозначает ли точка пересечения графиков момент встречи этих тел?

2. Итог урока Закончить предложение.

Я узнал, что...

Теперь я могу.

На основе.

Следовательно,.

V. Домашнее задание

1. Выучить конспект урока; соответствующий параграф учебника. Повторить материал по математике про линейную функцию и ее график.

2. Решить задачи.

• Двигаясь равномерно прямолинейно, тело за 10 с прошло 500 см. За сколько часов это тело, двигаясь с той же скоростью и в том же направлении, преодолеет путь 60 км?

• Вдоль оси Ox движутся два тела, координаты которых изменяются согласно формулам: x1 = 5 + 2t и x2 = -4 + 5t. Как движутся эти тела? В какой момент времени тела встретятся? Найдите координату точки встречи.