УРОК № 3
Тема. Основные свойства числовых неравенств
Цель урока: добиться усвоения учащимися содержания основных свойств числовых неравенств и их последствий, а также способа доведения этих свойств. Выработать умения: воспроизводить содержание изученных свойств, следствий из них и их доказательства; применять свойства числовых неравенств и следствия из них для решения упражнений на сравнение буквенных выражений и на доведение соответствующих неравенств.
Тип урока: усвоение знаний, выработка первичных умений.
Наглядность и оборудование: опорный конспект № 3.
Ход урока
I. Организационный этап
Учитель проверяет готовность учащихся к уроку, настраивает их на работу.
II. Проверка домашнего задания
Ученики выполняют самостоятельную работу № 1 [8].
III. Формулировка цели и задач урока.
Мотивация учебной деятельности учащихся
На этом этапе урока уместным будет слово учителя о том, что:
· изучение любого математического понятия включает в себя изучение определения, свойств и признаков этого понятия (если такие существуют), а также вопрос о связи понятия, что изучается, с изученным ранее материалом;
· несмотря на достаточно большое внешнее различие, которое существует между равенствами и неровностями, они имеют очень много общих свойств (в этом месте уместно будет продемонстрировать несколько простейших примеров с числовыми равенствами и соответствующими числовыми неровностями), но при этом имеют существенные отличительные свойства (также можно привести несколько примеров с числовыми равенствами и неровностями).
Поэтому вполне логично будет сформулировать задачи на урок, как изучение свойств числовых неравенств (через их сравнение с соответствующими свойствами числовых равенств); доведение этих свойств с использованием изученного на предыдущих уроках определения, а также овладения учащимися приемов применения доказанных свойств для решения задач на доказательство неравенств.
Как вариант работы на этом этапе урока (при условии соответствующего уровня интеллектуальной активности учащихся) моделируем проблемную ситуацию (сравнить числа), решение которой невозможно без изучения свойств числовых неравенств. В этом случае задачей урока является решение противоречия между объемом знаний учеников, которые в них есть, и теми знаниями, которые являются необходимыми для решения поставленной задачи.
IV. Актуализация опорных знаний и умений учащихся
Устные упражнения
1. Сравните числа х и у, если разность х - у равно: 1) 8; 2) 0; 3) -1,5.
2. Докажите неравенство:
1) х - 3 > х - 4;
2) х2 + у2 ≥ 2ху;
3) b + 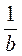 ≥ 2, b > 0;
≥ 2, b > 0;
4) 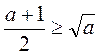 , а ≥ 0.
, а ≥ 0.
3. Является ли правильным утверждение:
1) если а = b, то b = а;
2) если а = b, b = с, то а = с;
3) если а = b, то а + с = b + с;
4) если а = b, то a - c = b - c;
5) если а = b, то ас = bс;
6) если а = b , то 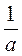 =
= 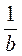 ?
?
V. Формирование знаний
План изучения нового материала
1. Основные свойства числовых неравенств.
2. Следствия из свойств числовых неравенств.
3. Примеры применения свойств числовых неравенств и следствий из них.
Опорный конспект № 3
Основные свойства числовых неравенств |
1. Если a > b, то b a. |
Доведение |
a > b 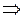 a - b > 0 a - b > 0 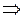 b - a = -(a - b) 0 b - a = -(a - b) 0 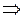 b a. b a. |
2. Если a b, b c, то a c. |
Доведение |
a b 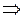 a - b 0; b c a - b 0; b c 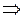 b - c 0, то есть (a - b) + (b - c)0. b - c 0, то есть (a - b) + (b - c)0.
(a - b) + (b - c) = a - b + b - c = a - c 0 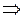 a c. a c. |
3. Если а b, а с - любое число, то а + с b + с. |
Доведение |
a b 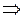 a - b 0; a - b = a + c - c - b = (a + c) + (b + c) 0 a - b 0; a - b = a + c - c - b = (a + c) + (b + c) 0 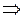 a + c b + c. a + c b + c. |
4. Если a b, c > 0, то ac bи с 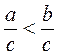 . .
Если а b, с 0, то ас > bc; 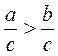 . . |
Доведение |
a b 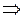 a - b 0; ac - bc = c(a - b), причем если с > 0, то с(а - b) 0, а если с 0, то с(а - b)>0. a - b 0; ac - bc = c(a - b), причем если с > 0, то с(а - b) 0, а если с 0, то с(а - b)>0.
Следовательно, если а b и с > 0, то ас bc; c 0, то ас > bс.
Неровности 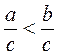 и и 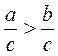 доказываем аналогично. доказываем аналогично. |
Следствия из свойств числовых неравенств |
1. Если а b + с, то а - с b. |
Доведение
a b + c 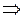 a - (b + c) 0, тогда а - b - с = (а - с) - b 0, то есть а - с b. a - (b + c) 0, тогда а - b - с = (а - с) - b 0, то есть а - с b. |
2. Если а > 0 и b > 0, и a b, то 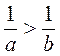 . . |
Доведение
a b 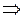 a - b 0. a - b 0. 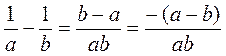 . .
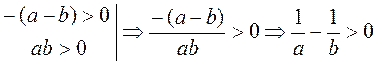 . .
|
Пример. Известно, что а b. Сравним значения выражений: 2а + 3 и 2b + 5. |
Решение
а b | ∙ 2; поскольку 2 > 0, то 2а 2b | + 3; 2а + 3 2b + 3.
3 5 | + 2b; поскольку 2 > 0, то 2b + 3 2b + 5.
Итак, 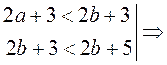 2а + 3 2b + 5. 2а + 3 2b + 5. |
Методический комментарий
Одним из важнейших базовых умений учащихся, предусмотренных программой по математике, является умение производить аргументированные рассуждения относительно оценки значений выражений. Работу по выработке таких умений было начато на предыдущих двух уроках, однако на этих уроках для аргументации действий учащихся были использованы только определение сравнения чисел и в отдельных случаях опорные неравенства. На данном уроке учащиеся должны взять на вооружение более широкий перечень способов, представленных основными свойствами числовых неравенств. При формировании знаний учащихся о эти свойства следует обратить внимание на такие моменты, которые будут способствовать более сознательному усвоению учащимися учебного материала:
доказательство свойств числовых неравенств основывается на определении сравнение чисел (то есть ведется через сравнения с нулем разности левой и правой частей некоторой неровности);
содержание свойств желательно выложить как математическим языком (в виде серии логически связанных между собой неровностей), так и в словесной форме;
свойство 4 (см. опорный конспект № 3) выполняется в данном виде только в случае, когда числа положительные;
закрепление содержания каждой из доказанных свойств следует провести на определенном конкретном примере.
Исходя из выше сказанного, формирование знаний учащихся желательно провести с как можно более широким привлечением учащихся к работе по доказательству свойств числовых неравенств.
VI. Формирование умений
Устные упражнения
1. Сравните числа:
1) m и n, если n > m;
2) m + 3 и n + 3, если m > n;
3) 3m и 3n, если m > n;
4) m и k, если m > n; n > k.
2. Известно, что а > 5. Определите (с обоснованием), является правильной неравенство:
1) а + 4 > 9;
2) 3а > 15;
3) -а -5.
Письменные упражнения
Для реализации дидактической цели урока следует решить упражнения такого содержания:
1) сравнить значения выражений, содержащих переменные а и b, если известно, например, что а b;
2) используя свойства числовых неравенств, записать правильные числовые неравенства, вытекающие из данной числовой неравенства;
3) упражнения, обращенные к упражнениям, которые решались на уроке № 1;
4) доказать числовую неравенство, опираясь на свойства числовых неравенств.
Методический комментарий
Набор упражнений, который дается для закрепления знаний свойств числовых неравенств и выработки умений их применять для сравнения выражений, является традиционным. Традиционными остаются требования, которым должны следовать ученики во время решения этих упражнений. Такими обязательными требованиями являются:
· четкое и полное воспроизведение соответствующих свойств числовых неравенств во время комментирования учащимися своих действий при решении предложенных упражнений;
· обязательное пошаговое письменное обоснование действий при применении свойств числовых неравенств.
VII. Итоги урока
Контрольное задание
В приведенных утверждениях найдите и исправьте ошибки, учитывая, что m > n > 0, с > 0.
1) n m;
2) m + c n + с;
3) m + c n;
4) сm > n;
5) 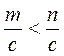 ;
;
6) 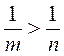 .
.
VIII. Домашнее задание
1. Изучить содержание и доказательство свойств числовых неравенств (см. опорный конспект № 3).
2. Решить упражнения на применение свойств числовых неравенств, аналогичные упражнениям классной работы.
3. На повторение: понятие двойного неравенства и упражнения на применение этого понятия.
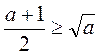
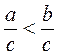
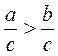
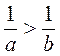
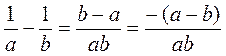 .
.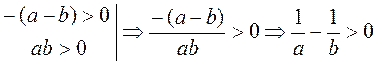 .
.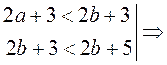
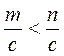
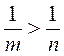 .
.