УРОК 3
Тема. Построение графиков функций с помощью геометрических преобразований известных графиков функций
Цель урока: Формирование умений строить графики функций с помощью восьми базовых преобразований графика функции
у = f(x): у = -f(x); у = f(-x); у = f(x) + b; у = f(x + a); у = af(x); у = f(ax); у = f(│x│); у = │f(x)│.
И. Проверка домашнего задания.
1. Решение упражнений, аналогичных домашних.
1) Найдите область определения функции: а) 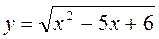 ; б)
; б) 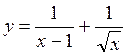 .
.
Решение
а) За то что арифметический квадратный корень существует только из неотрицательных чисел, х2 - 5х + 6  0 . Решим неравенство методом интервалов (найдем нули функции g = х2 - 5х + 6, нанесем их на координатную прямую и определим знак функции на каждом промежутке) (рис. 15).
0 . Решим неравенство методом интервалов (найдем нули функции g = х2 - 5х + 6, нанесем их на координатную прямую и определим знак функции на каждом промежутке) (рис. 15).
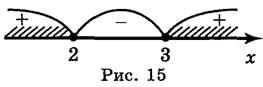
Следовательно, D(y) = (-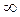 ; 2]
; 2]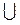 [3; +
[3; +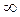 ).
).
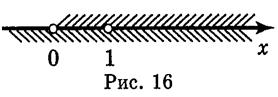
б) D(y) находим решив систему 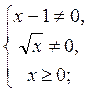
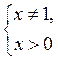 . Следовательно, D(y) = (0; 1)
. Следовательно, D(y) = (0; 1)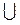 (1; +
(1; +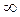 ) (рис. 16).
) (рис. 16).
а) За то что D(f) = R и f(-x) = (-х)(2(-х) - (-х)3) = х2(-2х + х3) = -x2(2x - х3) = -f(x), f(x) = x2(2x -х3) - нечетная.
б) За то что D(f) = R и 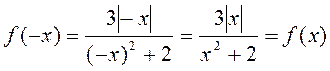 , то
, то 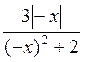 - парная.
- парная.
II. Повторение и систематизация знаний учащихся о геометрических преобразованиях графиков.
Запас функций, графики которых вы умеете строить, пока небольшой. Но используя известные из курсов геометрии и алгебры сведения о преобразовании фигур, этот список можно существенно расширить. Вспомним элементарные преобразования графика функции у = f(x) с помощью таблицы 2.
Таблица 2
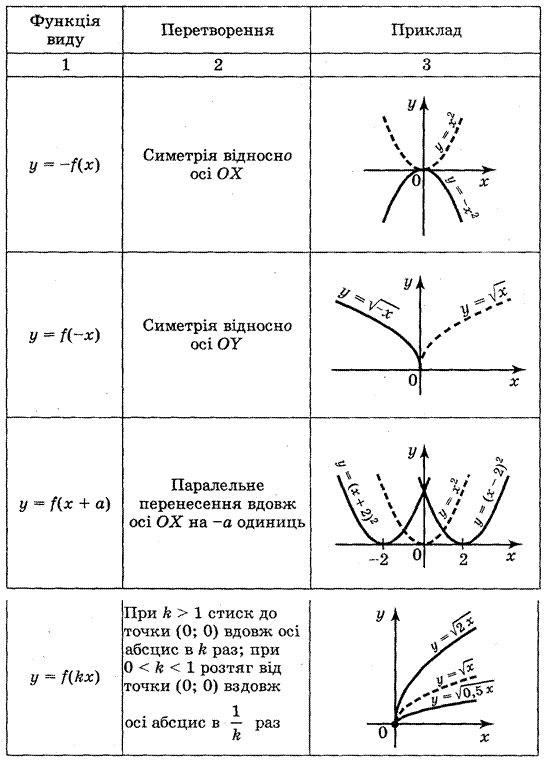
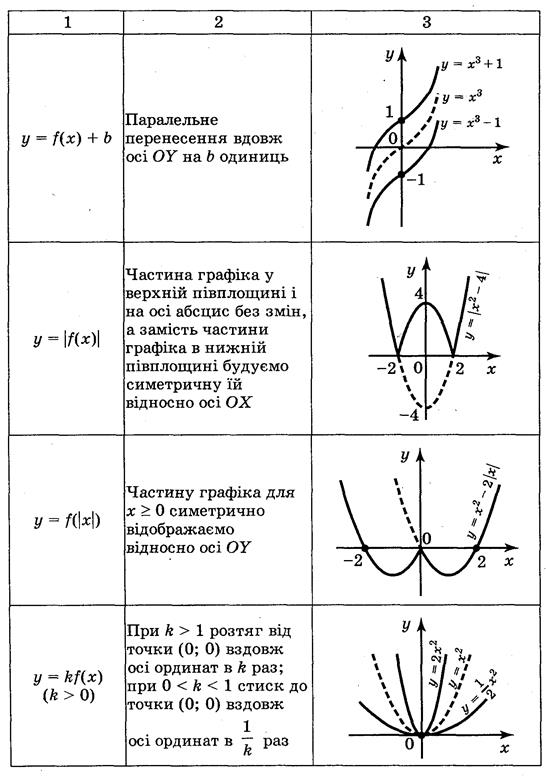
III. Формирование умений строить графики с помощью геометрических преобразований известных графиков
Коллективное выполнение упражнений№ 3 (1; 2; 3; 14; 19).
IV. Итог урока
V. Домашнее задание
Раздел И § 1 (3). Вопросы и задания для повторения № 27-31. Упражнение№ 3 (7, 8, 9, 4, 5, 6, 18).