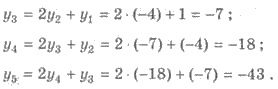АЛГЕБРА И НАЧАЛА АНАЛИЗА
Раздел III. ФУНКЦИЯ
§13. ЧИСЛОВЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ.
6. Числовые последовательности, заданные рекурентно.
Последовательность можно задавать,
определив первый или несколько первых членов последовательности, а затем - формулу, по
которой можно определить другие члены последовательности через предыдущие. Поэтому формулу
называют рекурентною, а способ задания последовательности - рекурентним.
Пример 1. Найдите второй, третий
и четвертый члены последовательности (xn), заданной
рекурентно: 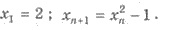
Решения. Имеем 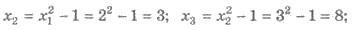
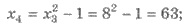
Пример 2. Найдите третий, четвертый и пятый члены последовательности
(вn), заданной
рекурентно: 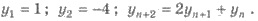
Решения. Имеем