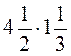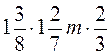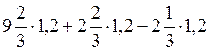Урок № 28
Тема. Задачи на умножение дробей
Цель: закрепить знание алгоритма нахождение дроби (процента) от числа и отработать навыки выполнения заданий, предусматривающих умножения дробных чисел.
Тип урока: применение знаний, навыков и умений.
Ход урока
I. Проверка домашнего задания
Индивидуальные задания
1. Нескольким учащимся можно предложить решить домашние задачи у доски (условие заранее записать на доске).
2. Фронтальная работа
1) Найдите:  ;
; 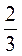 ;
; 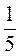 ;
; 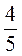 ;
; 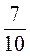 ;
; 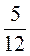 от 120 см3.
от 120 см3.
2) Найдите: 1 %; 5; 10; 35; 108; 110; 160; 200 от 800 г. Сравните полученные ответы с 800 г.
3) В саду 40 деревьев. Среди них есть яблони и груши. Сколько в саду яблонь, если: а) яблонь 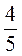 всех деревьев; б) груш
всех деревьев; б) груш 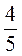 всех деревьев; в) яблони составляют 20 % всех деревьев; г) груши составляют 40 % всех деревьев?
всех деревьев; в) яблони составляют 20 % всех деревьев; г) груши составляют 40 % всех деревьев?
4) Выполните действия: 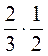 ;
; 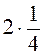 ;
; 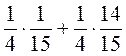 ;
; 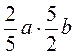 .
.
II. Актуализация опорных знаний
Вопрос к классу
1. Как найти дробь от числа? Приведите пример. Составьте задачу.
2. Как найти проценты от числа? Приведите пример. Составьте задачу.
@ Следует обратить внимание учащихся на то, что дробь / процент от числа можно взять любой. Но в задачах, если речь идет о части целого, дробь (сумма дробей), на который делится число, не превышает 1 (100 %).
III. Отработка навыков
@ На уроке следует обратить внимание на решение именно таких задач, в которых рассматривается часть от целого, что сводится к 1.
1. Экскаватор вырыл траншею длиной 150 м за 3 дня. За первый день он вырыл 40 % траншеи, а за второй - 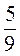 той части, что осталась. Сколько метров траншеи экскаватор вырыл за третий день?
той части, что осталась. Сколько метров траншеи экскаватор вырыл за третий день?
2. Велосипедист за час преодолел 40 % дистанции, а за вторую - 70% оставшейся дистанции. Сколько процентов дистанции проехал велосипедист за эти 2 часа?
3. Автотуристы проехали 520 км за 4 дня. За первый день они проехали 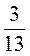 , за второй -
, за второй - 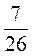 всего пути, а за третий - на 40 км меньше, чем за четвертый. Сколько километров проехали автотуристы за четвертый день?
всего пути, а за третий - на 40 км меньше, чем за четвертый. Сколько километров проехали автотуристы за четвертый день?
Дополнительные задачи
4. Один кран заполняет ванну за 15 мин, а второй - за 12 мин. Или наполнится ванна за 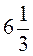 мин совместной работы кранов?
мин совместной работы кранов?
5. Увеличьте число 100 на 20 %, а полученное при этом число уменьшите на 20 %.
@ Желательно показать ученикам два способа решения этих задач.
1-й способ
В именованных величинах |
2-й способ
В дробях |
Грузовой автомобиль проехал 240 км за 4 ч. Какой путь проедет за это время легковой автомобиль, скорость которого составляет 120 % скорости грузового автомобиля?
1) 150 · 0,4 = 60 (м) - за 1-й день;
2) 150 - 60 = 90 (м) - останется после 1-го дня;
3) 90 · 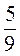 = 50 (м) - за 2-й день; = 50 (м) - за 2-й день;
4) 90 - 50 = 40 (м) - по 3-й день. Ответ. 40 м |
Вся траншея 100 % = 1.
1) 100 % - 40 % = 60 % - остаток после 1-го дня;
2) 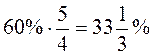 - за 2-й день; - за 2-й день;
3) 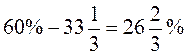 - по 3-й день; - по 3-й день;
4) 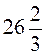 % от 150: 150· % от 150: 150·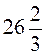 :100 = = :100 = =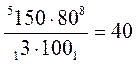 (м) - по 3-й день. (м) - по 3-й день.
Ответ. 40 м |
IV. Итоги урока
Самостоятельная работа
Вариант 1
1. а) Вычислите: 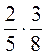 ;
; 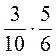 ;
; 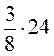 ;
; 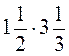 ; б) Упростите выражение
; б) Упростите выражение 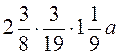 ; в) Вычислите
; в) Вычислите 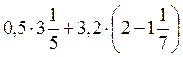 .
.
2. Решите задачи:
а) 1 кг печенья стоит 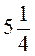 грн. Сколько будет стоить
грн. Сколько будет стоить 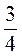 кг;
кг; 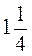 кг, 200 г этого печенья?
кг, 200 г этого печенья?
б) Турист преодолел за три дня 32 км. За первый день он прошел 37,5 % пути, за второй день 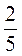 остатка. Сколько километров пути преодолел турист за 3 дня?
остатка. Сколько километров пути преодолел турист за 3 дня?
Вариант 2
1. а) Вычислите: 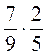 ;
; 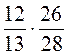 ;
; 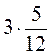 ;
; 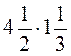 ; б) Упростите выражение:
; б) Упростите выражение: 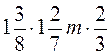 ; в) Вычислите
; в) Вычислите 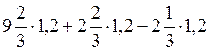 .
.
2. Решите задачи:
а) Какое расстояние преодолеет поезд со скоростью 75 км/ч за 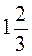 ч? за
ч? за 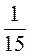 час? за 2 ч 36 мин?
час? за 2 ч 36 мин?
б) За три дня выплатили 480 грн. За первый день 12,5 % этой суммы, за второй день - 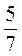 остатка. Сколько денег потратили за третий день?
остатка. Сколько денег потратили за третий день?
V. Домашнее задание
1. Длина комнаты 6 м, ее ширина составляет 75 % длины, а высота - 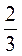 ширине. Найдите массу воздуха в этой комнате, если 1 м3 воздуха имеет массу 1,29 кг.
ширине. Найдите массу воздуха в этой комнате, если 1 м3 воздуха имеет массу 1,29 кг.
2. В магазин завезли 1,2 т картофеля. За первый день продали 0,2 всего картофеля, а за второй -  остатка. Сколько килограммов картофеля продали за второй день?
остатка. Сколько килограммов картофеля продали за второй день?
3. Уменьшите число 200 на 10%, а полученное при этом число увеличьте на 10%.
4. Задача. Сначала прошли 30 % всего пути, а затем 20 % остатка.
5. Сколько процентов пути осталось пройти?
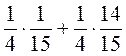 ;
; 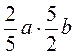 .
.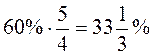
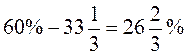
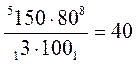 (м)
(м) 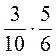 ;
; 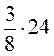 ;
; 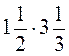
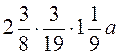
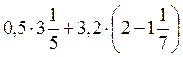
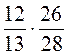 ;
; 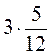 ;
;