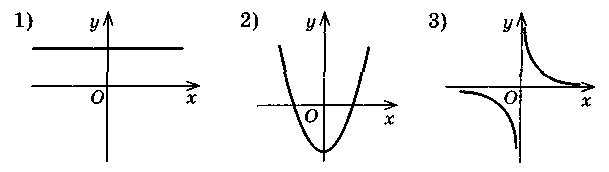УРОК № 28
Тема. График уравнения с двумя переменными
Цель урока: добиться усвоения учащимися содержания: определение графика уравнения с двумя переменными; схемы действий для построения графика уравнения с двумя переменными.
Выработать умения: воспроизводить содержание изученного определения и алгоритма; применять их для решения упражнений на построение графиков уравнений с двумя переменными.
Тип урока: обобщение и систематизация знаний, выработки умений.
Наглядность и оборудование: опорный конспект № 18.
Ход урока
I. Организационный этап
Учитель рассказывает о примерное содержание учебного материала данного раздела; количество учебных часов; ориентировочные даты проведения тематической контрольной работы и требования к знаниям и умениям учащихся.
II. Проверка домашнего задания
Учитель проверяет выполнен учениками анализ тематической контрольной работы № 3.
III. Формулировка цели и задач урока.
Мотивация учебной деятельности учащихся
На этом этапе урока уместны слова учителя о том, что материал предыдущего раздела «Функция и ее свойства» может быть использован не только для решения квадратных неравенств и задач, предусматривающих их решения, но и для решения других задач. В частности, если обратиться к материалу, изученному учащимися на уроках геометрии (уравнение фигуры в декартовых координатах), то становится понятным, что функции и их графики является одним из средств отыскание множеств точек, координаты которых удовлетворяют определенное уравнение с двумя переменными. Такую задачу учащиеся уже решали на уроках алгебры в 7 классе (при изучении темы «График линейного уравнения с двумя переменными»). Итак, на данном уроке встает вопрос о дополнении и систематизацию знаний и умений учащихся относительно содержания понятия «график уравнения с двумя переменными» и умения выполнять построения графика уравнения с двумя переменными и решать простейшие задачи на его применение.
IV. Актуализация опорных знаний и умений учащихся
Устные упражнения
1. Даны выражения:
а) х2 + в; б) ху + 3; в) у(х + 2).
Найдите значение каждого из данных выражений:
1) при х = -1, у = 2;
2) при x = -0,5, y = 0,4;
3) при x = -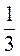 , у = 3.
, у = 3.
2. Даны функции:
а) у = - 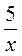 ; б) у = х2 - 2; в) у = 3х + 1; г) у = -2.
; б) у = х2 - 2; в) у = 3х + 1; г) у = -2.
Установите соответствие между данными функциями и графиками:
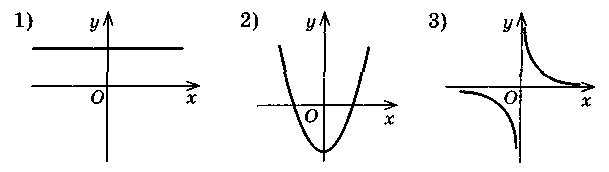
3. Выразите одну переменную через другую из равенства:
1) 4х - у = 1;
2) ху = 2;
3) х2 + у = 0;
4) х + ху = 2.
V. Формирование знаний
План изучения нового материала
1. Содержание понятия «уравнение с двумя переменными» и сопутствующих понятий.
2. Определение графика уравнения с двумя переменными. Степень уравнения с двумя переменными.
3. Схема действий при построении графика уравнения с двумя переменными.
Опорный конспект № 18
Уравнения с двумя переменными
Примеры: х2 + у2 = 25, ху = 4, х + ху = 1. |
Сопутствующие понятия |
1. Решение уравнения с двумя переменными х и у - это упорядоченная пара (х; у), которая превращает уравнение в верное равенство. |
Например, пара (2; 3) является решением уравнения ху = 6, так как при х = 2 и y = 3 данное уравнение имеет вид 2 ∙ 3 = 6, т.е. образуется правильная равенство. |
2. Степень целого уравнения с двумя переменными р(х; у) = 0 определяется как степень многочлена Р(х; у), если он сведен к стандартному виду. Например, х2 + ху + у = 0 - уравнение второй степени. |
График уравнения с двумя переменными х и у - это множество точек координатной плоскости с координатами (х; у), где пара (х; у) является решением данного уравнения с двумя переменными. |
Как построить график уравнения с двумя переменными
1. Если уравнение можно свести к виду (х - a)2 + (y - b)2 = R2, где а, b - произвольные числа, a R > 0, то графиком этого уравнения будет круг с центром (а; b) и радиусом R. |
2. В других случаях (если нет модуля) выражаем у через х и строим график созданной функции y = f(x). |
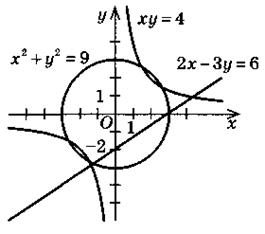
Пример. Построим график уравнения: 1) 2x - 3у = 6; 2) х2 + у2 = 9; 3) ху = 4. |
Решения (см. рисунок)
|
1) 2х - 3у = 6 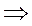 у = у = 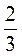 х - 2 - линейная функция. х - 2 - линейная функция. |
|
х |
0 |
3 |
|
|
|
y |
-2 |
0 |
|
2) х2 + у2 = 9 = 32 - уравнение окружности с центром (0;0) и радиусом 3.
3) ху = 4; у = 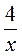 - обратная пропорциональность. - обратная пропорциональность. |
|
х |
-4 |
-2 |
-1 |
1 |
2 |
4 |
|
|
в |
-1 |
-2 |
-4 |
4 |
2 |
1 |
|
|
Методический комментарий
Основная часть учебного материала урока - это сведения и умения, которые учащиеся получили при изучении алгебры в предыдущих классах. На данном уроке проводятся преимущественно повторение, обобщение и систематизация учебного материала.
VI. Формирование умений
Устные упражнения
1. Является решением уравнения х2 + у = 10 пара чисел:
1) x = 3, в = 1;
2) (-2; 6)?
2. Принадлежат ли точки A(-2; 3); B(0; 0); С(3; 0) графику уравнения:
1) ху = -6;
2) х2 - у = 9;
3) х2 + у2 = 9?
3. Определите степень уравнения:
1) ху - 2у = 5;
2) х2 - у = 2;
3) х2 + 3у2 = 0.
4. Что является графиком уравнения:
1) х2 + у2 = 4;
2) (x - 1)2 + (y + 3)2 = 9;
3) х = 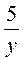 ; 4) х = 3у - 1?
; 4) х = 3у - 1?
Письменные упражнения
Для реализации дидактической цели урока следует решить упражнения такого содержания:
1) определить, является ли данная пара чисел решением уравнения с двумя переменными;
2) построить график уравнения с двумя переменными;
3) найти несколько решений уравнения с двумя переменными аналитически и по графику уравнения с двумя переменными;
4) на повторение: решить системы линейных уравнений с двумя переменными.
Методический комментарий
Для лучшего усвоения учащимися содержания материала урока рекомендуется при выполнении соответствующих упражнений неоднократно повторять определение решения уравнения с двумя переменными, графика уравнения с двумя переменными, алгоритм построения графика уравнения с двумя переменными (см. опорный конспект № 18).
VII. Итоги урока
Контрольные вопросы
1. Приведите примеры уравнений с двумя переменными различных видов.
2. Что называется решением уравнения с двумя переменными? Для каждого из приведенных в п. 1 уравнений найдите хотя бы одно из решений (если они есть).
3. Приведите примеры уравнений с двумя переменными, графиками которых являются:
1) круг;
2) прямая;
3) гипербола;
4) парабола.
4. Какое общее свойство имеет любая точка графика данного уравнения с двумя переменными?
VIII. Домашнее задание
1. Изучить определения понятий, рассмотренных на уроке.
2. Решить упражнения на построение графиков уравнений с двумя переменными.
3. Повторить способы решения систем линейных уравнений с двумя переменными (по справочнику для 7 класса); решить системы линейных уравнений с двумя переменными различными способами.