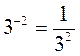Урок № 24
Тема. Определение степени с целым отрицательным показателем
Цель: добиться усвоения учащимися содержания определение степени с целым отрицательным показателем (для целой и дробной основы степень); сформировать умение воспроизводить определение степени и применять его для преобразования степени с целым отрицательным показателем в дробь, и наоборот, сформировать умение решать упражнения на вычисление значений числовых выражений с применением изученного определение степени с целым показателем.
Тип урока: усвоение знаний и первичных умений.
Наглядность и оборудование: опорный конспект «Степень с целым отрицательным показателем».
Ход урока
I. Организационный этап
II. Проверка домашнего задания
Учитель собирает тетради для проверки выполнения учащимися анализа тематической контрольной работы за розданными решениями (см. выше).
III. Формулировка цели и задач урока, мотивация учебной деятельности учащихся
Традиционно представление о возможности существования степени с целым отрицательным показателем формируется в связи с расширением понятия степени с натуральным показателем. Однако сознательному пониманию необходимости такого расширения могут способствовать, во-первых, обращение к справочной литературе, содержащей записи значений некоторых констант в стандартном виде с отрицательным показателем, а во-вторых, выполнение логических упражнений на сравнение и обобщение. Например, можно предложить ученикам продолжить числовые ряды (один из которых состоит из значений степеней некоторого числа, а второй состоит из самых соответствующих степеней):
1-й ряд: 1000, 100, 10, и, 0,1, 0,01, 0,001, ...
2-й ряд 103, 102, 101, 100, ...
После выполнения сравнения на этапе обобщения формулируется проблема - между существующим представлениям о степени (с натуральным показателем) и необходимыми для вычислений потребностями. Преодоление этого противоречия является одновременно и мотивом, и целью учебной деятельности учащихся на уроке.
IV. Актуализация опорных знаний и умений
@ С целью успешного восприятия учащимися учебного материала перед его изучением следует активизировать знания и умения учащихся: определение степени с натуральным показателем; основное свойство степени и ее последствия, а также их применение для вычисления значений числовых выражений и преобразования выражений, содержащих умножение, деление степеней с одинаковыми основаниями и возведение степени, произведения и частного выражений в степень.
Выполнение устных упражнений
1. Представьте в виде произведения дробей: 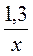 ;
; 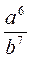 ;
; 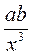 ;
; 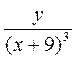 .
.
2. Прочитайте выражения, назвав основание и показатель степени; 64; (2,1)9; 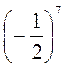 .
.
3. Вычислите значения выражений:
а) возведите в квадрат: 3; -5; 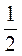 ;
; 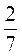 ;
; 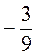 ; 0,8;
; 0,8;
б) возведите в куб: 2; -3; 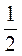 ;
; 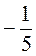 ;
; 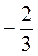 ; - 0,3.
; - 0,3.
4. Определите знак выражения, назвав основание и показатель степени: 64; (2,1)9; 101; (-7)5; 012; 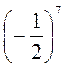 .
.
5. Определите знак выражения, не выполняя возведение в степень: 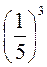 ;
; 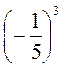 ; (-2)10; -210; (-3)9; -39;
; (-2)10; -210; (-3)9; -39; 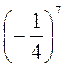 ;
; 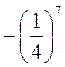 .
.
6. Укажите порядок действий в вычислении значения выражений: 152 - 34; 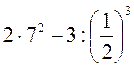 ; (32 - 23)20.
; (32 - 23)20.
V. Усвоение знаний
План изучения нового материала
1. Определение степени с целым отрицательным показателем.
2. Запись определение степени с целым отрицательным показателем для случая основы, которая имеет вид 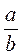 .
.
3. Примеры применения определение степени с целым отрицательным показателем для вычисления значения выражения, содержащего степень.
Конспект 7 |
|
Степень с целым отрицательным показателем. Стандартный вид числа |
|
1 |
Если п - натуральное число (n > 2) и а - любое число, то
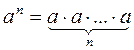
Замечания: a1 = a, 1n = 1, 0n = 0 для любого а |
|
|
|
|
2 |
Если n - целое отрицательное (обратное натуральному числу) и а ≠ 0, то 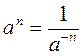 или если n - натуральное, то или если n - натуральное, то 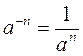
Замечание: a0 = 1, для а ≠ 0 |
|
|
|
|
3 |
Свойства: если m, n - целые числа и а ≠ 0, b ≠ 0, то: |
|
|
аm ∙ аn = аm + n |
(аm)n = аmn |
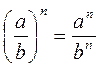
|
|
|
аm : аn = аm - n |
(аb)n = anbn |
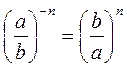
|
|
|
|
|
4 |
Если число k > 0 записанное в виде:
k = а ∙ 10n, где 0 а 10, n - целое число, то говорят, что k записанное в стандартном виде, где n - порядок числа k |
|
|
|
|
5 |
Умножение и деление чисел, записанных в стандартном виде:
если k1 = а ∙ 10n, k2 = b ∙ 10m, то
а) k1 ∙ k2 = (а ∙ 10n) ∙ (b ∙ 10m) = (ab)(10n+m);
б) 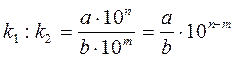 . .
Замечание: произведение и частное чисел k1 и k2, записанных в стандартном виде, также после выполнения действий следует записать в стандартном виде |
|
|
|
|
@ После проведенной работы на этане определение цели урока достаточно обобщить проведенные наблюдения и сформулировать их в виде формулы 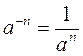 , n
, n  N, где а ≠ 0, (а также, возможно, в словесном виде: степень с целым отрицательным показателем и с основой, отличной от нуля, равна дроби, числитель которой - единица, а показатель - степень с тем же основанием и противоположным данном (натуральным показателем; однако требовать от учащихся воспроизведения этой формулировки не следует). При этом необходимо обратить особое внимание учащихся на то, что степень с целым отрицательным показателем имеет смысл только при ненулевом значении основы степени, поэтому, в отличие от степени с натуральным показателем, степень числа 0 с целым отрицательным показателем не имеет смысла (см. опорный конспект).
N, где а ≠ 0, (а также, возможно, в словесном виде: степень с целым отрицательным показателем и с основой, отличной от нуля, равна дроби, числитель которой - единица, а показатель - степень с тем же основанием и противоположным данном (натуральным показателем; однако требовать от учащихся воспроизведения этой формулировки не следует). При этом необходимо обратить особое внимание учащихся на то, что степень с целым отрицательным показателем имеет смысл только при ненулевом значении основы степени, поэтому, в отличие от степени с натуральным показателем, степень числа 0 с целым отрицательным показателем не имеет смысла (см. опорный конспект).
Поскольку для решения многих задач полезным является определение степени с целым отрицательным показателем, записанное на случай, если основа с дробью вида 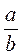 , поэтому сразу по окончании рассмотрения примеров на прямое применение определение степени с целым отрицательным показателем учитель или предлагает учащимся в виде задачи, или вместе с учащимися выводит определение степени с целым отрицательным показателем для степени с основой
, поэтому сразу по окончании рассмотрения примеров на прямое применение определение степени с целым отрицательным показателем учитель или предлагает учащимся в виде задачи, или вместе с учащимися выводит определение степени с целым отрицательным показателем для степени с основой 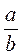 (а ≠ 0, b ≠ 0):
(а ≠ 0, b ≠ 0): 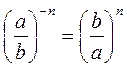 . Рассматривая вопрос о сфере возможного применения изученного определение, следует обратить внимание учащихся на гой факт, что вычисление значений выражений, содержащих среди других арифметических действий действие возведение числа в степень, следует помнить о существующем порядке выполнения действий различной степени, а также о том, что во время вычисления значения степени с целым отрицательным показателем сначала применяется определение степени, а затем вычисляется значение степени с натуральным показателем (по определению степени с натуральным показателем).
. Рассматривая вопрос о сфере возможного применения изученного определение, следует обратить внимание учащихся на гой факт, что вычисление значений выражений, содержащих среди других арифметических действий действие возведение числа в степень, следует помнить о существующем порядке выполнения действий различной степени, а также о том, что во время вычисления значения степени с целым отрицательным показателем сначала применяется определение степени, а затем вычисляется значение степени с натуральным показателем (по определению степени с натуральным показателем).
VI. Формирование умений
Выполнение устных упражнений
1. Вычислите: 24; (-3)2; (0,1)3; (-1)8; 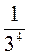 ;
; 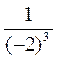 ; (-15)9; 0,30;
; (-15)9; 0,30; 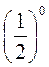 ; 00.
; 00.
2. Замените дробью степень с целым отрицательным показателем. Заполните пропуски: 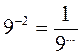 ;
; 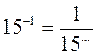 ;
; 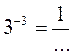 ;
; 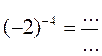 .
.
3. Замените дробь степенью с целым отрицательным показателем: 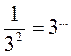 ;
; 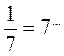 ;
; 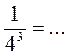 ;
; 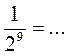
Выполнение письменных упражнений
Для реализации дидактической цели на этом уроке следует решить задачи следующего содержания:
1. Запись степени с целым отрицательным показателем в виде дроби и наоборот.
1) Замените степень с целым отрицательным показателем дробью: а) 10-6; б) 9-2; в) -1; г) х-20; д) (ab)-3; в) (а + b)-4.
2) Замените дробь в степень с целым отрицательным показателем: а) 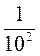 ; б)
; б) 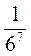 ; в)
; в) 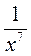 ; г)
; г) 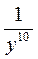 ; д)
; д) 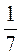 .
.
2. Запись числа в виде степени с заданной основой.
1) Подайте числа 4, 8, 16, 32, 2, 1, 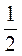 ,
,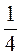 ,
, ,
,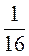 в виде степени с основанием 2.
в виде степени с основанием 2.
2) Подайте числа:
а) 8, 4, 2, 1, 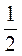 ,
, 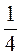 и
и  в виде степени с основанием 2;
в виде степени с основанием 2;
б) 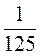 ,
, 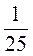 ,
, 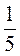 , 1, 5, 25, 125 в виде степени с основанием 5.
, 1, 5, 25, 125 в виде степени с основанием 5.
3. Вычисление значений числового выражения (то имеет вид степени с целым отрицательным показателем или содержит такой степень).
1) Вычислите: 9-2; 15-1; 3-3; 5-4; 120; (-2)-4; (-3)-3; 0,5-2.
2) Найдите значение выражения:
а) 5 ∙ 102; б) 16 ∙ 2-5; в) 5-3 : 250; г) 3 : 2-3; д) 2-4 +2-2; е) 2-3 - 2-4; ж) 6-1 + 3∙3-2; с) 4-1 - 3-2.
3) Найдите значение выражения:
а) 256 ∙ 2-8; б) 0,1-2 + (-1)-24; в) 1,5-3 : 2,5-2; г) 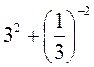 ; д)
; д) 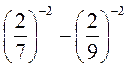 ; е)
; е) 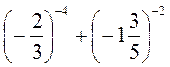 .
.
4) Найдите значение выражения:
а) 1-1 + 2-1 + 3-1 + 4-1; б) 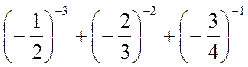 ; в)
; в) 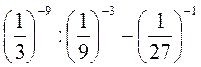 ; г) (2 + 2-1)-2 - (2 + 2-2)-1.
; г) (2 + 2-1)-2 - (2 + 2-2)-1.
4. Сравнение с нулем значение выражения.
1) Сравните с нулем значение степени:
а) 9-5; б) 2,6-4; в) (-7,1)-6; г) (-3,9)-3.
5. Запись в виде рациональной дроби выражения с переменными, содержащего степень с целым отрицательным показателем.
1) Представьте выражение в виде рациональной дроби: a) 4а-2b-1; б) 7-1ab-5; в) х-2в-3; г) (а + b)-2.
2) Упростите выражение:
а) (а + 5)-2(3а + 15); б) (а-2 - b-2) : (a + b); в) (b - 4)-1 - (b + 4)-1; г) (x-3 - y-3) : (х2 + ху + y2); д) 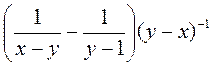 ; е)
; е) 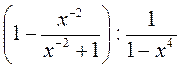 .
.
6. Логические упражнения и задачи повышенного уровня сложности для учащихся, имеющих достаточный и высокий уровни знаний.
1) Представьте в виде дроби выражение: а) ху-2 - х-2у; б) 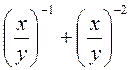 ; в) mn(n - m)-2 - (m - n)-1; г) (х-1 + у-1)(х-1 - в-1).
; в) mn(n - m)-2 - (m - n)-1; г) (х-1 + у-1)(х-1 - в-1).
2) Упростите выражение: а) 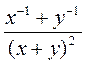 ; б)
; б) 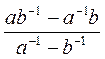 .
.
3) выражение пропущено?
7. На повторение использование свойств степени с натуральным показателем:
1) Запишите в виде одночлена стандартного вида выражение: а) -5х3у2 ∙ 2ху3; б) (-3a2b4)2; в) (-2xy5)3; г) (m4n3)2 ∙ (-mn)3.
2) Найдите значение выражения: а) 55 ∙ 23; б) 44 ∙ 1,254 ∙ 24; в) 0,59 ∙ (23)2; г) 2,55 ∙ 0,72 ∙ 0,45.
@ Упражнения к уроку направленные на усвоение учащимися сформулированного определения, а также на формирование умения переходить от записи, содержащий целый отрицательный показатель, к записи, содержащий дробь (с противоположным натуральным показателем), и наоборот. Этому будет способствовать выполнение учащимися упражнений с прямым указанием на выполнение указанных действий и вычисление значения выражения, а также исследовательские упражнения (см. выше).Розв'язання упражнений на повторение - на применение свойств степени с натуральным показателем - способствовать подготовке учащихся к изучению соответствующих свойств степени с целым отрицательным показателем.
VII. Итоги урока
В любом из случаев правильно выполнено действие?
а) 3-2 = 32; б) 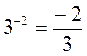 ; в)
; в) 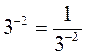 ; г)
; г) 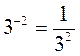 .
.
VIII. Домашнее задание
1. Изучить определение степени с целым отрицательным показателем, а также свойства, полученные во время выполнения письменных упражнений.
2. Решить упражнения на применение определения и сформулированных на уроке свойств.
3. Повторить основное свойство степени с натуральным показателем и ее последствия, решить упражнения соответствующего содержания.
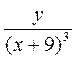 .
.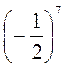 .
.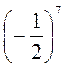 .
.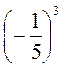 ; (-2)10; -210; (-3)9; -39;
; (-2)10; -210; (-3)9; -39; 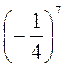 ;
; 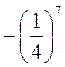 .
.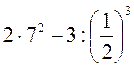 ; (32 - 23)20.
; (32 - 23)20.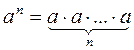
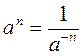 или если
или если 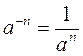
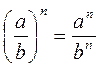
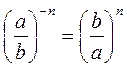
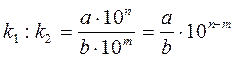
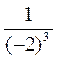 ; (-15)9; 0,3
; (-15)9; 0,3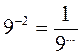
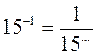
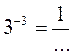
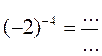
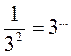
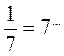
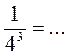
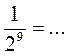
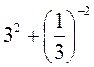 ; д)
; д) 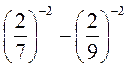 ; е)
; е) 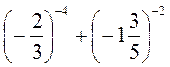 .
.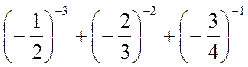 ; в)
; в) 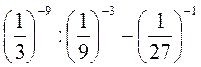 ; г) (2 + 2-1)-2 - (2 + 2-2)-1.
; г) (2 + 2-1)-2 - (2 + 2-2)-1.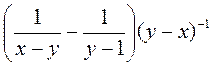 ; е)
; е) 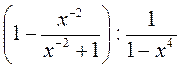 .
.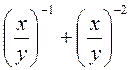 ; в)
; в) 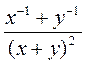 ; б)
; б) 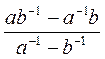 .
.
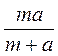 (
( (
(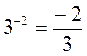 ; в)
; в) 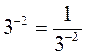 ; г)
; г)