АЛГЕБРА И НАЧАЛА АНАЛИЗА

Раздел II. УРАВНЕНИЯ И НЕРАВЕНСТВА

§28. ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ.

4. Уравнения, сводящиеся к простейшим с помощью формул логарифмирования.

При решении более сложных логарифмических уравнений можно придерживаться следующей схемы:

1) Находим ОДЗ уравнения.

2) С помощью формул логарифмирование сводим уравнение к виду span lang=EN-US style='font-family:"Verdana","sans-serif"'>log_af(x) = b или вида log_af(x) = log_ag(x).

3) Решаем полученное уравнение.

4) Проверяем корни на предмет вхождения в ОДЗ исходного уравнения и даем ответ.

Пример 1. Решите уравнение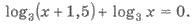

Решения. ОДЗ уравнения найдем с системы 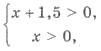т.е. х > 0.

Имеем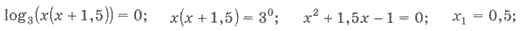

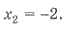
ОДЗ уравнения удовлетворяет только первый корень. Следовательно, х = 0,5 - единственный корень уравнения.

Пример 2. Решите уравнение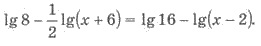

Решения. ОДЗ уравнения найдем из системы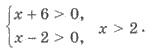

Домножимо левую и правую части уравнение на 2, чтобы избавиться от дробей:

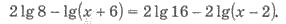
Используем формулу логарифмирования:

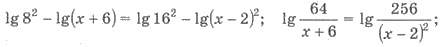
Тогда 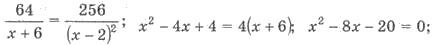x₁ = 10; х₂ = -2. ОДЗ уравнения удовлетворяет только первый корень. Следовательно, x = 10 - единственный корень уравнения.