Все тела в природе взаимно притягиваются. Закон, описывающий это притяжение, открыл И. Ньютон. Его называют законом всемирного тяготения. По этому закону любые две материальные точки притягиваются друг к другу с силой, прямо пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между ними:

где G - коэффициент пропорциональности, который называют гравитационной постоянной. Для определения силы взаимодействия тел, которые не могут рассматриваться как материальные точки, их надо разделить на точечные элементарные массы Δm, найти значение силы взаимодействия каждой элементарной массы одного тела с элементарными массами другого, а потом добавить эти силы.

В случае произвольных тел, то есть тел различной плотности и формы, решения такой задачи достаточно сложное. Эта задача упрощается для однородных шаров и таких тел, в которых массу условно можно сосредоточить в одной точке. Для таких тел можно применить закон всемирного тяжести в виде (2.23).

Гравитационные силы сравнительно слабые. Например, они значительно слабее электрические. Поэтому процессы внутри атома определяются практически только электрическими силами (если не учитывать внутриядерная процессы).

Гравитационные силы становятся ощутимыми для тел больших масс и космических тел - планет, звезд и т.д. Масса Солнца в 750 раз больше, чем суммарная масса всех планет Солнечной системы. Поэтому планеты значительно больше притягиваются Солнцем, чем друг другом. Например, Луна является естественным спутником Земли и на него больше всего влияет поле ее притяжения. Центр масс Солнечной системы смещен от центра Солнца всего на 2,15R Солнца (радиус Солнца 695 989 км, расстояние центра Солнца от центра масс Солнечной системы около 1 486 000 км).

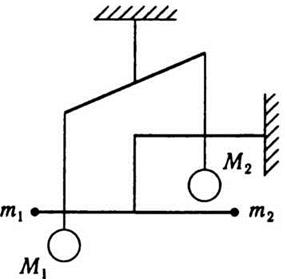
Рис. 2.5 Рис. 2.6

Для определения гравитационной силы взаимодействия между телами по закону Ньютона (2.23) надо знать гравитационную постоянную G. Впервые экспериментально определил 1798 г. Г. Кавендиш. Он измерил силу притяжения между свинцовыми пулями по помощью крутильных весов. Схематично основную часть прибора изображен на рис. 2.5. На одном стержни подвешены две массивные свинцовые пули, на втором - две небольшие свинцовые шарики. Всю установку помещали в специальную камеру и защищали от колебаний температуры. Поворачивая стержень с большими шарами, можно было наблюдать, что стержень с маленькими шариками, который подвешен на нитке с известными упругими свойствами, поворачивается на некоторый угол навстречу тяжелым пулям. По углом закручивания подвеса Г. Кавендиш подсчитывал суммарную силу притяжения 2F между шарами М₁ и m₁ и m₂ и m₂. Расстояние между центрами шаров точно измерялась. Определена Г. Кавендишем величина G отличалась лишь на 1 % от той, которую достали в следующих опытах.

В 1898 г. Ріхарц к 100-летию опыта Г. Кавендиша по идее Ф. Жолли определил гравитационную постоянную другим способом. Схему опыта Рихарца представлены на рис. 2.6. До конца коромысла весов подвешены два шарика А и В, имеющие одинаковые массы (с учетом подвеса). Свинцовая плита массой 100 т своим притяжением увеличивает вес шарика А и уменьшает вес шарики В. Поэтому весы отклоняются от положения равновесия. По отклонению коромысла весов можно судить о силе притяжения между шарами и свинцовой плитой. Этот способ определение G считается наиболее точным. Установлено, что

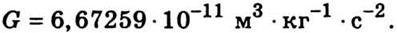
Используя закон всемирного притяжения (2.23), можно найти зависимость ускорения свободного падения от высоты над поверхностью Земли. Действительно, вес тела связана с его массой соотношением

Если пренебречь влиянием суточного вращения Земли, то по закону тяготения вес тела определяется по формуле

где М₃ - масса Земли; m - масса тела; r - расстояние тела от центра Земли, равной радиусу Земли (R₃ = 6 378 164 м), если тело лежит на ее поверхности. Из формулы (2.25) видно, что вес тела уменьшается с удалением тела от земной поверхности. Поскольку масса тела остается постоянной, то эта закономерность обусловлена характером поведения ускорения свободного падения от высоты. Если приравнять соотношение (2.24) и (2.25), то получим аналитическое выражение этой зависимости

где R₃ - радиус Земли.