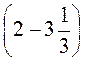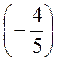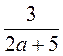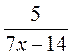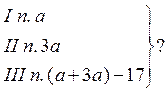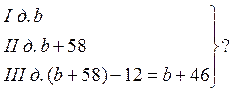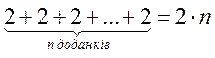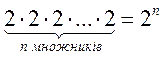АЛГЕБРА
Уроки для 7 классов
Урок № 18
Тема. Выражения. Тождества
Цель: проверить уровень усвоения знаний и качества производимых умений, предусмотренных программой по теме.
Тип урока: контроль знаний, умений (тематическая контрольная работа).
Ход урока
И. Условие тематической контрольной работы
Вариант 1 |
Вариант 2 |
№ 1. Упростите выражение:
4(5а - 3b) - (-b + 2а). |
№ 1. Упростите выражение
3(4х - 2z) - (5z + 10х). |
№ 2. Найдите значение выражения:
4 : (-0,8) - 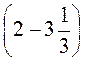 . . |
№ 2. Найдите значение выражения
0,35 · 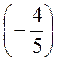 - - 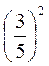 . . |
№ 3. Докажите тождество:
7(4 - a) - 3(-3а + 1) - 25 = 2а. |
№ 3. Докажите тождество
9,8b = 5 + 9b - 1,2b - 2(2,5 - b). |
№ 4. При каких значениях переменной имеет смысл выражение 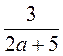 ? ? |
№ 4. При каких значениях переменной имеет смысл выражение 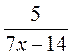 ? ? |
№ 5. Упростите выражение и найдите его значение:
0,5(1,6 х - 6,4 в) - 2,4(1,5 х + у),
если х = 3, у = -4,5. |
№ 5. Упростите выражение и найдите его значение:
1,5(-2,4 а + 3,8b) - 1,6(2,5 а - b),
если а = 2; b = -3. |
№ 6. На первой полке стоит а книг, на второй - втрое больше, чем на первой, а на третьей - на 17 книг меньше, чем на первой и второй полках вместе. Запишите в виде выражения число книг на трех полках вместе. Вычислите при а = 20. |
№ 6. За первый день магазин продал b кг сахара, за второй - на 58 кг больше, чем за первый, а за третий - на 12 кг меньше, чем за второй. Запишите в виде выражения количество килограммов сахара, проданного магазином за три дня. Вычислите при b = 45. |
№ 7*. Докажите, что сумма трехзначного числа и удвоенной суммы его цифр делится на 3. |
№ 7*. Докажите, что шестицифове число, в записи которого первые три цифры одинаковые и последние три цифры одинаковые, делится на 37. |
II. Решения и ответы
Вариант 1 |
Вариант 2 |
№1. 4(5а - 3b) - (-b + 2а) = 20а - 12b + b - 2а = 18а - 11b. |
№1. 3(4х - 2z) - (5z + 10x) = 12x - 6z - 5z - 10x = 2x - 11z. |
№2. 4 : (-0,8) - 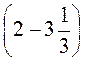 = -5 - = -5 - 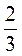 = -5 = -5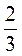 . . |
№2. 0,35 · 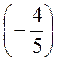 - - 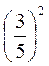 = -0,28 - 0,36 = -0,64. = -0,28 - 0,36 = -0,64. |
№3. 7(4 - а) - 3(-3а + 1) - 25 = 28 - 7а + 9а - 3 - 25 = 2а. |
№3. 5 + 9b - 1,2b - 2(2,5 - b) = 5 + 9b - 1,2b - 5 + 2b = 9,8b. |
№ 4. 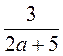 имеет смысл при всех а, кроме а = -2,5, потому что при а = -2,5 2а + 5 = 0. имеет смысл при всех а, кроме а = -2,5, потому что при а = -2,5 2а + 5 = 0. |
№ 4. 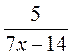 имеет смысл при всех х, кроме х = 2, при х = 2 7х - 14 = 0. имеет смысл при всех х, кроме х = 2, при х = 2 7х - 14 = 0. |
№ 5. 0,5(1,6 х - 6,4 в) - 2,4(1,5 х + у) = 0,8 х - 3,2y - 3,6 х - 2,4y = -2,8 х - 5,6y.
Если х = 4, у = -4,5, то
-2,8 х - 5,6 у = -2,8 · 3 - 5,6 · (-4,5) = -8,4 + 25,2 = 16,8. |
№ 5. 1,5(-2,4 а + 3,8b) - 1,6(2,5 а - b) = -3,6 а - 5,7b - 4а + 1,6b = -7,6 а - 3,9b.
Если а = 2, b = -3, то
-7,6 а - 3,9b = -7,6 · 2 - 3,9 · (-3) = -15,2 + 11,7 = -3,5. |
№6. 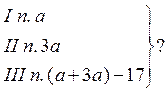
а + 3а + ((а + 3а) - 17) = 4а + 4а - 17 = 8а - 17.
Если a = 20,
то 8а - 17 = 8 · 20 - 1 7 = 143. |
№6. 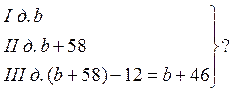
b + (b + 58) + (b + 46) = 3b + 104.
Если b = 45, то 3b + 104 = 3 · 45 + 104 = 135 + 104 = 239.
|
№7. 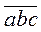 + 2(а + b + с) = 3х, где х-целое. + 2(а + b + с) = 3х, где х-целое.
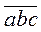 + 2(а + b + с) = 100а + 10b + с + 2а + 2b + 2с = 102а + 12b + 3с = + 2(а + b + с) = 100а + 10b + с + 2а + 2b + 2с = 102а + 12b + 3с =
= 3 · 34а + 3 · 4b + 3с = 3(34а + 4b + с) - целое, натуральное. Следовательно,
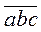 + 2(a + b + c) делится на 3. + 2(a + b + c) делится на 3.
|
№7.  = 37 · х, где х-целое (натуральное). = 37 · х, где х-целое (натуральное).
 = 100000a + 10000a + 1000a + +100b + 10b + b = 111000а + 111b = = 100000a + 10000a + 1000a + +100b + 10b + b = 111000а + 111b =
= 111(1000a + b) = 37 · 3 · (1000а + b) - натуральное, потому что а, b - цифры, поэтому  делится на 37. делится на 37. |
III. Итог урока. Рефлексия
- Какое задание тематической работы было самым сложным? Которое было самым легким?
- Чего не хватило для успешного решения задач?
Правильные ответы на задания...
IV. Домашнее задание
№ 1. Из текста контрольной работы (текст выдается ученикам домой) выпишите и решите задачи, которые вызвали трудности. Если решение не получается (не знаем пути, не можем найти ошибки и др.), записать вопрос.
№ 2. Опережающее домашнее задание. По алгоритму сравнения выполните сравнение выражений (разное, общее, создайте группы по признаку сходства):
2 + 2 + 2 = 2 · 3; 2 · 2 · 2 = 23; 2 + 2 = 2 · 2; 2 · 2 · 2 · 2 = 24; 2 + 2 + 2 + 2 = 2 · 4;
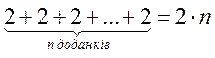 ; ; 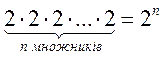 . .
|
|