УРОК № 19

Тема. Построение правильных многоугольников

Цель урока: ознакомление учащихся с правилами построения правильных многоугольников (в частности треугольников, четырехугольников и шестиугольников).

Тип урока: комбинированный.

Требования к уровню подготовки учащихся: строят правильный треугольник, четырехугольник и шестиугольник.

Ход урока

И. Проверка домашнего задания

Двое учащихся воспроизводят по откидными досками решения домашних задач 1 и 2, а в это же время класс пишет математический диктант.

Задача 1. Решение

Пусть сторона квадрата, вписанного в круг, равна х. Поскольку имеем один и тот же круг, то R = 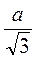и R = .

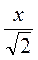Отсюда = ; .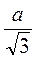

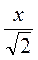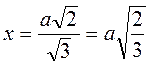Ответ. .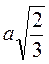

Задача 2. Решение

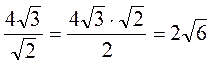Если радиус круга равен 4 см, то сторона вписанного треугольника равна 4 см. Учитывая, что сторона квадрата равна 4 см, радиус круга, описанного вокруг квадрата, равна (см).

Ответ. 2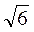 см.

Математический диктант.

Дан круг, радиус которого равен:

вариант 1 - 6 см; вариант 2 - 8 см.

Найдите:

а) сторону правильного треугольника, вписанного в этот круг;

б) сторону правильного треугольника, описанного вокруг этого круга;

в) сторону правильного четырехугольника, описанного вокруг данного круга;

г) сторону правильного четырехугольника, вписанного в данный круг;

д) сторону правильного шестиугольника, вписанного в данный круг;

есть) периметр правильного шестиугольника, описанного вокруг этого круга.

Ответы

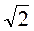Вариант 1. а) 6 см; б) 12 см; в) 12 см; г) 6 см; д) 6 см; в) 24 см.

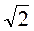Вариант 2. а) 8 см; б) 16 см; в) 16 см; г) 8 см; д) 8 см; в) 32 см.

II. Решение задач

Коллективное решение задач

1. 1) Конец винта газовой задвижки имеет правильную трехгранную форму. Какой наибольший размер может иметь каждая грань, если диаметр цилиндрической части винта равна 2 см?

Решение

Каждая грань может иметь наибольший размер, если конец винта газовой задвижки, который имеет форму правильного треугольника, будет вписан в круг диаметром 2 см. Следовательно, сторона треугольника равна: R= 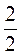∙ = (см).

Ответ. см.

1. 2) Докажите, что сторона правильного 12-угольника вычисляется по формуле а12 = 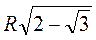, где R - радиус описанного круга.

Доведение

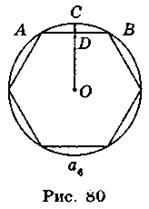
Пусть АВ - сторона вписанного правильного шестиугольника (рис. 80). АС - сторона вписанного правильного 12-угольника. Из прямоугольного треугольника ACD имеем:

АС = 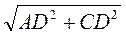, где AD = = ,

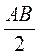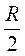CD = OC - OD = R -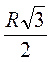

Тогда АС = 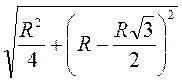= = 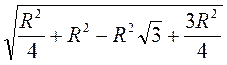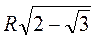что и требовалось доказать.

III. Самостоятельная работа

Самостоятельная работа обучающего характера предложена в двух вариантах. Двое учащихся выполняют работу за откидными досками, а остальные - в тетрадях. После окончания выполнить проверку с записями, сделанными на откидных досках.

Вариант 1

1. 1. Сторона правильного многоугольника равна а, а радиус описанного вокруг него круга R. Найдите радиус вписанной окружности.
2. 2. Выразите сторону b правильного описанного около окружности многоугольника через радиус R окружности и сторону а правильного вписанного многоугольника с тем же числом сторон.

Вариант 2

1. 1. Сторона правильного многоугольника а, а радиус вписанной в него окружности r. Найдите радиус описанного круга.
2. 2. Выразите сторону а правильного вписанного в круг многоугольника через радиус R окружности и сторону b правильного описанного многоугольника с тем же числом сторон.

Решение заданий самостоятельной работы

Вариант 1

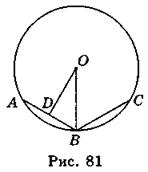
1. 1. Пусть АВ = ВС = а, OB = R (рис. 81), OD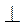AB, тогда BD = 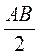= 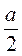. Из треугольника ODB имеем:

OD = = .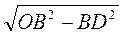

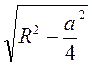Ответ. .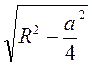

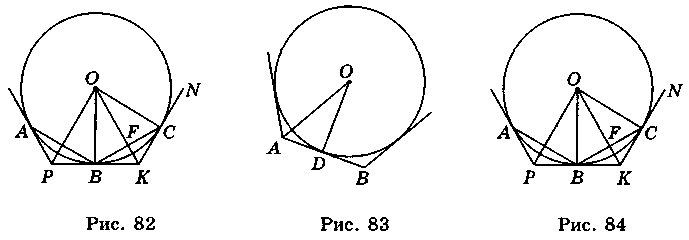
1. 2. Пусть ABC... - правильный вписанный многоугольник, a PKN... - правильный описанный многоугольник (рис. 82). Треугольники ОВС и ОРК подобные, поскольку они имеют равные углы. Из подобия треугольников имеем: 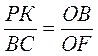. Отсюда РК = 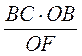= 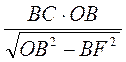. Учитывая, что ВС = а, OB = R, имеем:

.

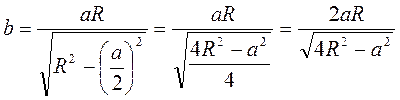Ответ. .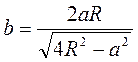

Вариант 2

1. 1. Пусть АВ = а, DO = r (рис. 83). OD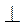AB, тогда AD = 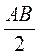= 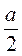. Из треугольника ADO имеем: АО = = .

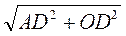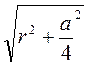Ответ. .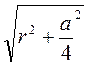

1. 2. Пусть ABC... - правильный вписанный многоугольник, a PKN... - правильный описанный многоугольник (рис. 84). ΔОВД 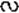ΔОРК, то есть 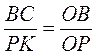. Отсюда ВС = 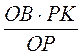= 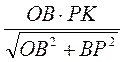. Учитывая, что PK = b, OB = R, имеем:

.

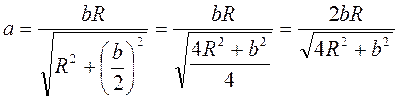Ответ. .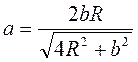

IV. Восприятие и осознание нового материала

Фронтальная беседа

1. 1) Как можно построить правильный шестиугольник?
2. 2) Построено правильный шестиугольник. Как на этом рисунке построить правильный треугольник?
3. 3) Как можно построить правильный четырехугольник?
4. 4) Как можно построить правильный восьмиугольник?

Выполнение упражнений

1. 1) Впишите в данное круг квадрат.
2. 2) Впишите в данный круг правильный шестиугольник.
3. 3) Впишите в данный круг правильный треугольник.
4. 4) Опишите вокруг круга правильный восьмиугольник.

Решение

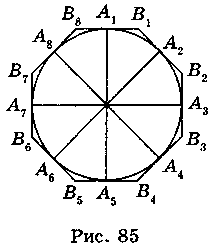
Делим круг на восемь равных частей. (Для этого проводим две взаимно перпендикулярные диаметры А1А5 и А3А7; четыре образованные дуги делим пополам (рис. 85).)

Через точки А1, А2, А3, А4, А5, A6, А7, A8 деления окружности на восемь частей проводим касательные к окружности. Образовавшийся многоугольник - описан правильный восьмиугольник.

V. Домашнее задание

Решить задачи.

1. 1. Конец валика диаметром 4 см обпилено в виде квадрата. Определите, какой наибольший размер может иметь сторона квадрата.
2. 2. Докажите, что сторона правильного шестиугольника рассчитывается по формуле а8 = R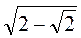, где R - радиус описанного круга.

VI. Подведение итогов урока

Вопрос к классу

1. 1. Как можно описать вокруг окружности правильный треугольник?
2. 2. Как можно описать вокруг окружности квадрат?
3. 3. Как можно построить правильный дванадцятикутник?
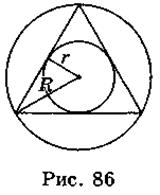
4. 4. Вокруг правильного треугольника описана окружность, и в этот самый треугольник вписанный круг (рис. 86). Радиус вписанного круга r, а радиус описанной окружности - R. Определите, какие из приведенных утверждений являются правильными, а какие - неправильными.

а) R = 2r.

б) Центр описанной окружности совпадает с точкой пересечения медиан треугольника.

в) Сторона треугольника равна R.

г) Сторона треугольника равна r.

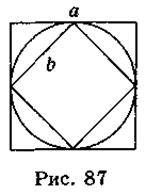
1. 5. В круг вписан квадрат, и вокруг этого самого круга описано квадрат (рис. 87). Сторона описанного квадрата равна а, а сторона вписанного квадрата - b. Определите, какие из приведенных утверждений являются правильными, а какие - неправильными.

а) a = b.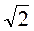

б) Центр окружности совпадает с точкой пересечения диагоналей вписанного квадрата.

в) Радиус окружности равен .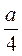

г) Радиус круга равен 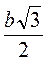.