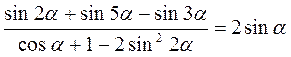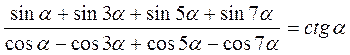|
Объяснение учителя 1. Выведем формулу преобразования суммы синусов в произведение. Обозначим 1) sin x + sin y = sin(α + β) + sin(α - β) = sin α · соs β + cos α · sиnβ + sin α · cos β - cos α · sиn β = 2sиn α · соs β = 2sиn Следовательно, сумма синусов равна удвоенному произведению синуса половину суммы на косинус піврізниці.
Для суммы косинусов имеем: 2) соs х + соs в = соs(α + β) + соs(α - β) = соs α соs β - sиn α sin β + cos α соs β + sиn α sиn β = 2 соs α соs β = 2 соs Следовательно, сумма косинусов равна удвоенному произведению косинуса половину суммы на косинус піврізниці.
Для разности косинусов имеем: 3) соs х - соs в = соs(α + β) - соs(α - β) = соs α соs β - sиn α sin β - cos α соs β - sиn α sиn β = - 2 sin α sin β = 2 sin Следовательно, разность косинусов равна числу, противоположному удвоенному произведению синуса половину суммы на синус піврізниці. 4) sin x - sin y = sin х + sin(-y) = 2 sin Следовательно, разность синусов равна удвоенному произведению синуса піврізниці на косинус половину суммы. 2. Для получения формул преобразования произведения в сумму выпишем подряд четыре формулы: sin(x + у) = sin x cos в + cos x sin у; (1) sin(x - у) = sin x cos в - cos x sin у; (2) cos(x + у) = cos x cos в - sin x sin у; (3) cos(x - у) = cos x cos в + sin x sin у. (4) Вычитая почленно из равенства (4) равенство (3), получим: cos(x - у) - cos(x + у) = 2 sin x sin или sin x sin у = Произведение синусов двух чисел равна піврізниці косинуса разности и косинуса суммы этих чисел.
Добавив почленно равенства (4) и (3), имеем: соs(x - у) + соs(х + у) = 2 соs x соs или cos x cos y = Произведение косинусов двух чисел равна полусумме косинуса разности и косинуса суммы этих чисел.
Добавив почленно равенства (1) и (2), получим sin(x - у) + sin(х + у) = 2 sin x cos или sin x cos у = Произведение синуса одного числа на косинус второго числа равна полусумме синуса разности и синуса суммы этих чисел.
Выполнение упражнений 1. Упростите выражения: а) б) в) sиn α · г) Ответ: а) 2. Вычислите: а) соs 22° - соs 38°; б) sin 5° + sin 55°. Ответ: а) sиn 8°; б) соs 25°. 3. Преобразуйте в произведение: а) соs 2α + соs 14α + соs 6α + соs 10α; б) sin 4β + sin 10β + sin 22β + sin 16β . Ответ: а) 4соs 2α соs 4α соs 8α; б) 4 соs 3β соs 6β sиn 13β. 4. Докажите тождество: а)
IV. Подведение итогов урока
V. Домашнее задание Раздел И § 10 (5, 6). Вопросы и задания для повторения раздела И № 69-70. Упражнения№ 52 (8; 15), № 53 (8; 15; 16)
|
|
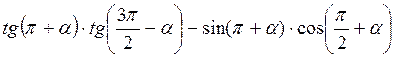 ;
;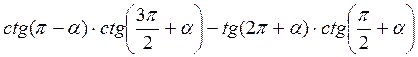 ;
;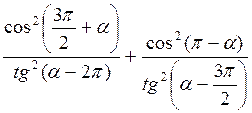 ;
;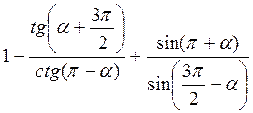 .
.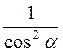 ; в) 1; г)
; в) 1; г) 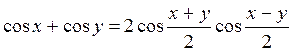
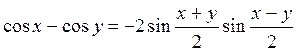
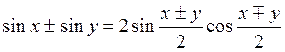 ;
; 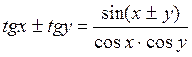 .
.
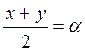 ,
, 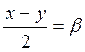 , тогда
, тогда 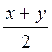 со
со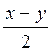 .
. 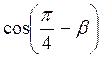 -
- 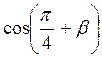 ;
; 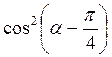 -
- 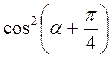 ;
;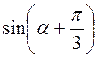 ;
; 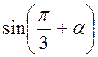 +
+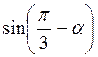 .
.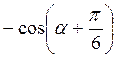 ; г)
; г)