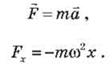КОЛЕБАНИЯ И ВОЛНЫ. ОПТИКА
1. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ
1.2. ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ
1.2.1. УРАВНЕНИЕ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ
При гармонических колебаниях изменение
колебательной величины со временем происходит по закону синуса или косинуса (рис.
2):
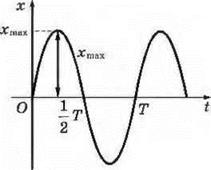
Рис. 2
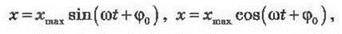
где
х - мгновенное значение колебательной величины (смещение от положения равновесия);
хmax - максимальное значение колебательной
величины или амплитуды колебаний (А);
ωt - фаза колебания. Это угловая величина, которая определяет
долю периода (в градусах или радианах), прошла от начала колебания: при
описании колебания через синус - от ближайшего момента, когда величина имела
нулевое значение; при описании колебания через косинус - от ближайшего момента,
когда величина имела максимальное значение;
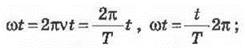
φ0 - начальная фаза, т. е. значение
фазы колебания в момент начала отсчета времени (t0).
Свободные колебания удобнее описывать
функцией косинуса, поскольку cos 0° = 1.
Вынужденные колебания удобнее
описывать функцией синуса, поскольку sin
0° = 0:
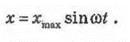
Скорость гармонических колебаний -
первая производная координаты по времени:
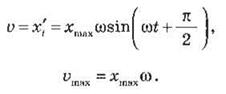
Ускорение гармонических колебаний -
первая производная скорости по времени, вторая производная координаты по времени:
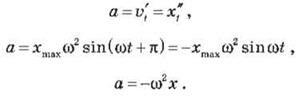
Гармоническое колебание - такое
колебания, ускорение которого пропорциональное величине смещения х и имеет противоположный
ему направление:
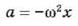
Общая закономерность: если какая-то
величина изменяется по закону синуса или косинуса, то скорость ее изменения
происходит по тому же закону, но с амплитудой (максимальным значением), в
ω раз большей, и с фазой, на π/2 - в большей.
Сила, что предопределяет гармоничные
колебания, прямо пропорциональна абсолютному
смещение тела от положения равновесия и направлена противоположно смещению: