АЛГЕБРА И НАЧАЛА АНАЛИЗА

Раздел II. УРАВНЕНИЯ И НЕРАВЕНСТВА

§4. МЕТОДЫ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ.

2. График линейного уравнения с двумя переменными.

Графиком уравнения с двумя переменными х и в называют фигуру, состоящую из всех точек координатной плоскости, координаты которых являются решениями этого уравнения.

Графиком уравнения ах + bу = с, в котором хотя бы один из коэффициентов а или b отличен от нуля, является прямая. Для построения графика такого уравнения достаточно найти координаты двух точек этого графика, отметить эти точки на координатной плоскости и провести через них прямую.

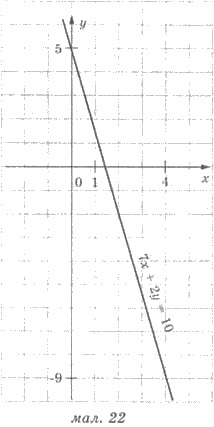
Пример 1. Построить график линейного уравнения с двумя переменными 7х + 2у = 10.

Решения. Выразим переменную у через переменную х: 2у = 10 - 7х ; у = 5 - 3,5 х. Составим таблицу соответствующих значений для некоторых двух точек:

График уравнения 7х + 2у = 10 представлены на рисунке 22.

Полезно также помнить следующее.

1) Чтобы построить график уравнения у = m, достаточно обозначить на оси в точку (0;m) и провести через эту точку прямую, параллельную оси х.

2) Чтобы построить график уравнения х = n, достаточно обозначить на оси х точку (n;0) и провести через эту точку прямую, параллельную оси у.

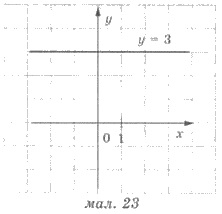
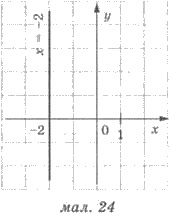
На рисунке 23 изображен график уравнение 0х + 2у = 6 , которое после упрощений превращается в уравнение у = 3. На рисунке 24 - график уравнения-5х + 0y = 10, которое после упрощений превращается в уравнение х = -2.