Часть 4

ОПТИКА. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ

Раздел 14 СКОРОСТЬ РАСПРОСТРАНЕНИЯ СВЕТА. ОСНОВЫ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ

14.8. Динамика специальной теории относительности

Мы рассмотрели исключительно пространственно-временные соотношения, кинематику теории относительности. Теперь ознакомимся с релятивистской динамикой.

Степени взаимодействия одного тела с другим есть сила. Масса тела вводится как индивидуальная стала характеристика, измеряется инертностью тела. Важным этапом в развитии механики стало введение более абстрактных понятий: импульс (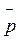 = m) и кинетической энергии тела (Е = mυ² /2).

Импульс и кинетическая энергия - две различные меры движения. Кинетическая энергия как величина скалярная характеризует движение только с количественной стороны, импульс как величина векторная показывает еще и направление движения. Классическая динамика основана на втором законе Ньютона, который утверждает, что изменение импульса пропорциональна действующей силе и происходит в направлении действия силы:

К тому же, как утверждает опыт, переход от системы К к системе К', движущейся относительно системы К с постоянной скоростью и в направлении оси х (см. рис. 14.5), сопровождается изменением компонентов силы по следующим формулам:

Несохранение силы при переходе от одной инерциальной системы к другой обусловлен тем, что длины отрезков в направлении движения и промежутки времени, от которых зависят силы, меняются.

А. Эйнштейн доказал, что второй закон Ньютона (14.20) инвариантный преобразованиям Лоренца, если импульс тела в инерциальной системе отсчета определить так:

где m - масса тела; - скорость тела в выбранной системе отсчета; с - скорость света в вакууме.

Следовательно, в релятивистской динамике, как и в ньютоновской, импульс материальной точки пропорционален ее массе m и совпадает по направлению со скоростью этой точки. Однако в отличие от ньютоновской динамики импульс материальной точки есть нелинейной функцией ее скорости.

При этом принято считать, что масса m не зависит от скорости материальной точки и тем самым является інваріантною относительно выбора систем отсчета. Если υ « с, то выражение (14.22) практически равен ты, т.е. совпадает со значением импульса материальной точки в ньютоновской механике. Импульс 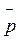, выраженный формулой (14.22), иногда называют релятивістським импульсом материальной точки*.

Таким образом, в релятивистской области между импульсом тела и скоростью уже нет пропорциональной зависимости, а существует более сложная зависимость, которая выражается формулой (14.22).

Второй закон Ньютона в релятивистской форме имеет следующий вид:

Из (14.22) видно, что Все реальные силы конечны, а их действие на тело ограничено по время. Поэтому согласно (14.23) они не могут предоставить телу бесконечно большой импульс. Следовательно, скорость тела относительно любой инерциальной системы отсчета не может быть равна скорости света в вакууме, а меньше от нее.

Это утверждение справедливо для атомов, молекул и всех элементарных частиц, за исключением фотонов, нейтрино и антинейтрино, масса которых равна нулю**, поэтому их скорость не может отличаться от скорости света в вакууме.

В отличие от ньютоновской механики сила 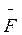, которая действует на материальную точку, не инвариантна относительно выбора инерциальной системы отсчета. Правила преобразования компонент силы при переходе от одной инерциальной системы отсчета к другой можно получить из условия ло- ренц-инвариантности уравнения (14.23). При малых скоростях (υ « с) уравнение (14.23) практически совпадает с основным уравнением ньютоновской динамики (2.7). Однако со увеличением скорости материальной точки на ее импульс растет быстрее, чем меняется скорость.

_____________________________________________________________

*До недавнего времени массу m обычно называли массой покоя материальной точки, а - релятивистской массой этой точки. Соответственно считали, что масса материальной точки зависит от ее скорости.

**В настоящее время тщательно изучается вопрос о возможности отличия от нуля значений масс нейтрино и антинейтрино.