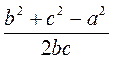Урок № 13
Тема. Определение трапеции. Отдельные виды трапеций
Цель: сформировать у учащихся понятие трапеции, ее элементов; рассмотреть определение рівнобічної и прямоугольной трапеций, содержание свойств углов трапеции, прилежащих к боковой стороне, и углов рівнобічної трапеции.
Формировать умения:
· воспроизводить выученные утверждение;
· выполнять рисунок по описанию;
· по готовым рисунком находить элементы трапеции;
· решать простейшие задачи на вычисление.
Тип урока: усвоение новых знаний.
Наглядность и оборудование: конспект «Трапеция. Виды трапеции».
Ход урока
I. Организационный этап
II. Проверка домашнего задания
Учитель собирает тетради учеников с выполненным анализом контрольной работы.
III. Формулировка цели и задач урока
С целью создания положительной мотивации учебной деятельности учащихся и формирование понимания логики изучения материала можно обратиться к схеме, составленной на уроке № 10.
По этой схеме предлагаем ученикам, пользуясь ранее полученными знаниями, ответить на вопросы.
1. Какая фигура называется четырехугольником?
2. Какое дополнительное условие надо знать, чтобы утверждать, что представленный четырехугольник является параллелограммом?
3. Правильно, что любой четырехугольник является параллелограммом?
4. Является ли четырехугольник параллелограммом, только две противоположные стороны которого параллельны? Выполните изображение такого четырехугольника. Отвечая на вопрос, учащиеся должны прийти к осознанию того факта, что:
· параллелограммы (изученные на предыдущих уроках) является лишь одним из по крайней мере двух видов выпуклых четырехугольников;
· кроме параллелограммов (которые имеют две пары параллельных сторон), существуют четырехугольники, у которых только одна пара параллельных сторон.
Таким образом, выделяется новый геометрический объект. Ввести определение этой фигуры, рассмотреть ее свойства, виды - основная цель урока.
IV. Актуализация опорных знаний
С целью сознательного понимания и дальнейшего усвоения учащимися содержания определения, свойств и признаков рівнобічної трапеции следует активизировать знания и умения относительно признаков и свойств параллельных прямых (пересечены третьей), признаков равенства прямоугольных треугольников, определение расстояния между параллельными прямыми (см. 7 класс), а также определение четырехугольника.
Выполнение устных упражнений
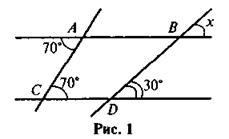
1. За. рисунком 1 найдите угол х.
2. Про три точки известно, что они находятся на одинаковом расстоянии от одной и той же прямой. Можно ли утверждать, что они лежат на одной прямой?
3. Как начертить две параллельные прямые на расстоянии 3 см друг от друга?
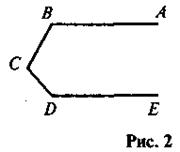
4. На рисунке 2 АВ || DE. Докажите, что  ABС +
ABС +  BCD +
BCD +  СDE = 360°.
СDE = 360°.
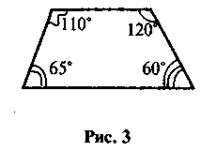
5. Правильно ли выполнен рисунок 3?
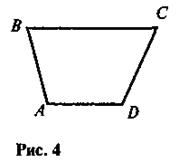
6. На рисунке 4 AD || ВС. Докажите, что  С +
С +  D = 180°.
D = 180°.
V. Усвоение знаний
План изучения нового материала
1. Определение трапеции. Элементы трапеции (основания, боковые стороны, углы, высоты).
2. Свойства углов трапеции, прилежащих к боковым сторонам; высот трапеции.
3. Прямоугольная трапеция: определение, свойство высот прямоугольной трапеции.
4. Равносторонняя трапеция: определение, свойства углов и диагоналей, признаки рівнобічної трапеции.
@ Если сравнивать содержание и последовательность изучения материала по новым учебником и по учебнику, который было рекомендовано использовать ранее (см. Геометрия. 7-9, А. В. Погорелов), то заметна существенная разница как в последовательности, так и в содержании предлагаемого учебного материала. А именно: в новом учебнике сначала предлагается изучить понятие трапеции и ее виды, а уже после этого изучается теорема Фалеса и ее применение при исчислении средней линии треугольника и трапеции. Такая последовательность изучения способствует формированию у учащихся целостного представления о понятие четырехугольника: более логично изучив понятие четырехугольника на выделив один из его видов (с двумя парами параллельных сторон), рассмотреть другой возможный случай (с одной парой параллельных сторон). А уже дальше более углубленно изучить особые свойства каждого из выделенных видов четырехугольников.
Если сравнивать содержание материала в новом учебнике он существенно расширен за счет введения в текст свойства углов при боковых сторонах трапеции, свойства высот трапеции, выделение двух видов (прямоугольной и рівнобічної) трапеции и введения понятия признаки рівнобічної трапеции (за углами и при основе)- Поскольку содержание материала, предложенного в учебнике, почти полностью соответствует плану изучения темы, то изучение нового материала на уроке можно организовать как самостоятельную работу учащихся по получению знаний.
В зависимости от уровня учебных достижений учащихся класса и при наличии времени можно рассмотреть такие утверждения (с доведением):
1) высота прямоугольной трапеции равна одной из ее боковых сторон;
2) диагонали рівнобічної трапеции уровне, и наоборот, если диагонали трапеции равны, то она равносторонняя;
3) сумма противоположных углов рівнобічної трапеции равна 180°;
4) диагонали рівнобічної трапеции образуют с ее основанием равные углы, и наоборот, если диагонали трапеции образуют с ее основанием равные углы, то трапеция равносторонняя;
5) высота рівнобічної трапеции, проведенные из вершины тупого угла, делит большее из основ на отрезки, один из которых равен полусумме оснований, а второй - піврізниці основ.
Поскольку объем нового материала в теме «Трапеция. Виды трапеций» является достаточно большим, то, в зависимости от уровня математической подготовки учащихся, планирование изучения раздела может быть разным: новый материал можно выложить на этом уроке, тогда на следующем уроке будет отработано его применения; или же на этом уроке изучить только содержание материала учебника и закрепить знания учащихся относительно его содержания, а на следующем уроке дополнить знания учащихся дополнительными свойствами и признаками (см. выше) и отработать навыки применения всех утверждений, изученных в теме «Трапеция. Виды трапеций».
Полное содержание учебного материала урока содержится в конспекте «Трапеция. Виды трапеций».
Конспект 5 |
Трапеция. Виды трапеций |
|
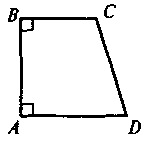
Определение. Четырехугольник, две стороны которого параллельны, а две другие непараллельные, называется трапецией
 
АС и BD - диагонали, ВК и TN - высоты |
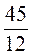
|
Свойства
Если ABCD - трапеция, основания ВС и AD, высоты ВК и TN, то:
1)  A + A +  B = B =  С + С +  D = 180°; D = 180°;
2) ВК = ТN |
|
Отдельные случаи трапеции |
|
а) Определение. Трапеция, одна из боковых сторон которой перпендикулярна к основаниям, называется прямоугольной
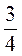 
|
|
Свойства
Если в трапеции ABCD BC || AD и  A = 90°, то АВ - высота трапеции A = 90°, то АВ - высота трапеции |
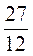
|
б) Определение. Трапеция с равными боковыми сторонами называется трапецией рівнобічною
 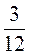
|
|
Свойства |
Признаки |
|
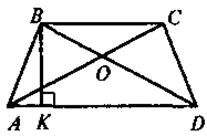
1) Если ABCD - равносторонняя трапеция с основаниями ВС и AD, то
а)  A = A =  D, D,  B = B =  С; С;
б)  A + A +  C = C =  B + B +  D= 180°; D= 180°;
в) AС = BD
г)  СAD = СAD =  BDA BDA |
1) Если в трапеции ABCD BC || AD,  A = A =  D, то D, то
ABCD - равносторонняя трапеция |
|
2) Если ABCD - равносторонняя трапеция. BC || AD, AB = CD i  BAC = BAC =  CAD, то АВ = ВС CAD, то АВ = ВС |
2) Если в трапеции ABCD BC || AD и AC = BD , то ABCD - равносторонняя трапеция |
|
3) Если ABCD - равносторонняя трапеция, BC || AD и  BCA = BCA =  DCA, то CD = AD DCA, то CD = AD |
3) Если в трапеции ABCD BC || AD и  CAD = CAD =  ADB, то ADB, то
ABCD - равносторонняя трапеция |
VI. Формирование первичных умений Выполнения устных упражнений
1. Найдите на рисунке 1 трапеции. Назовите их основания и боковые стороны.
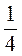
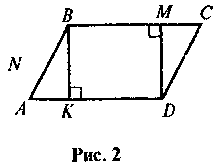
2. ABCD - параллелограмм (рис. 2). Сколько четырехугольников вы видите на рисунке? Есть среди них параллелограммы; трапеции?
3. Могут ли основания трапеции равны друг другу? Почему?
4. Могут ли соседние углы трапеции быть равными? Могут ли противоположные углы трапеции быть равными?
5. Обязательно ли углы трапеции, прилегающие к большему основанию, являются острыми? Приведите примеры.
6. Может равносторонняя трапеция быть прямоугольной?
7. Может высота трапеции быть больше боковую сторону? равна боковой стороне?
8. Диагонали трапеции ABCD (BC || AD) пересекаются в точке О.
а) может Ли треугольник AOD равен треугольнику ВОС?
б) может Ли треугольник АОВ равен треугольнику DOC?
9. Может ли точка пересечения диагоналей трапеции быть серединой каждой из них; одной из них?
Особое внимание следует обратить на упражнение № 3. Кроме предупреждения типичной ошибки учащихся (основы трапеции неровные), это задание имеет целью сообщить учащимся о наиболее распространенный способ изображения произвольной трапеции: сначала изображают два неравных параллельных отрезка, а затем их концы соединяют двумя другими отрезками.
Выполнение графических упражнений
1. Начертите параллелограмм ABCD и проведите в нем высоту СН.
а) Определите вид трапеции АВСН.
б) является высотой трапеции любая высота параллелограмма? Приведите контрпример.
2. Начертите равнобедренный треугольник AMD с основанием AD. Отметьте на стороне АМ точку и проведите через нее прямую, параллельную AD. Отметьте точку С - точку пересечения этой прямой со стороной МD.
а) Определите вид трапеции ABCD.
б) Проведите диагонали трапеции. Измерьте и сравните их длины.
Выполнение письменных упражнений
1. В рівнобедреній трапеции высота, проведенная из вершины тупого угла, делит большее основание на отрезки длиной 6 см и ЗО см. Найдите меньшее основание трапеции.
2. Найдите неизвестные углы:
а) трапеции ABCD с основаниями AD и ВС, если  A = 40°,
A = 40°,  D = 50°;
D = 50°;
б) рівнобедреної трапеции, один из углов которой равен 58°;
в) прямоугольной трапеции, наибольший угол которой втрое больше наименьший.
VII. Итоги урока
1. Могут ли длины оснований трапеции быть равными?
2. Может ли основание трапеции равно боковой стороне?
3. Могут ли быть равными углы трапеции, прилегающие к боковой стороне?
4. Какие общие свойства имеют трапеция и параллелограмм?
5. Существует трапеция, в которой: а) два противоположные углы равны; б) три угла острые?
6. Может ли сумма углов при меньшем основании трапеции быть больше суммы углов при большем основании?
VIII. Домашнее задание
Изучить содержание определений, теорем и их доказательства. Решить задачи.
1. Найдите неизвестные углы:
а) рівнобедреної трапеции, высота которой, проведенная из вершины тупого угла, образует с боковой стороной угол 22°;
б) прямоугольной трапеции, которую диагональ, проведенная из вершины тупого угла, делит на два равнобедренные прямоугольные треугольники.
2. Меньшая основа рівнобедреної трапеции равна 10 см. Найдите большее основание трапеции, если высота, проведенная из вершины тупого угла, делит ее на отрезки, один из которых равен 3 см.
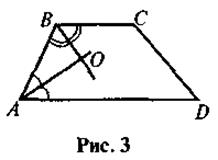
3. O - точка пересечения биссектрис углов А и В трапеции ABCD (рис. 3). Докажите, что  AOB = 90°.
AOB = 90°.