Корень n-ой степени и его свойства

Корнем n-й степени из числаа называется такое число, n-и степень которого равняется а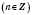. Если n - число нечетное, то существует - и к тому же только один - корень n-й степени из произвольного числа а. Этот корень - число того же знака, что число а, и равна 0, если .
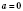
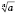
Обозначение: , где n - показатель корня, a - подкоренное выражение.
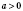
Пусть n - четное число. Если , то существует два противоположных числа, которые являются корнями n-й степени из а.
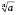
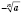
Обозначения: - положительный корень n-й степени из а, - противоположное ему число (n - четное).
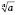
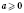
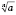
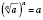
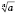
Выражение , если n - четное, имеет смысл для . Если n - нечетное, то выражение имеет смысл при любом а. для всех значений а, для которых имеет смысл.
Арифметическим корнем n-ой степенииз неотъемлемого числа называется неотрицательное число, n-и степень которого равняется а.
Для корней нечетного степени .
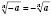
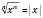
Для корней парного степени для любого значения х.
Для любого натурального n, целого k и неотрицательных чисел a и b верно:
.
.
.
.
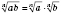
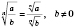
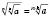
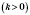
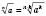
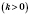
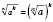
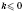
(если , a ≠ 0).
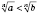
, если .
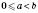