Некоторые способы решения тригонометрических уравнений
1. Уравнения, сводящиеся к квадратным
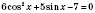
.
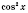
легко выразить через
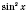
с помощью основной тригонометрической тождества
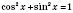
:
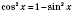
.
Следовательно,
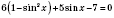
;
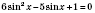
.
Пусть
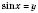
,
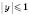
.
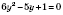
;
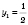
;
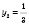
.
1)
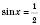
;
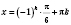
,
k Є
Z.
2)
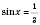
;
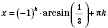
,
k Є
Z.
Ответ:
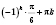
,
k Є
Z;
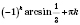
,
k Є
Z.
2. Способ разложения на множители
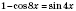
;
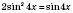
;
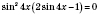
;
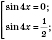
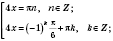
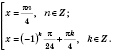 Ответ
Ответ:
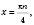 n
n Є
Z;
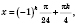 k
k Є
Z.
Если во время решения получаем совокупность нескольких серий решений, целесообразно проверить, нельзя их описать общей формулой. Для этого рекомендуется использовать тригонометрическое круг:
Например, обозначив на круге две серии:
видим, что ответ можно записать в виде
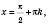 k
k Є
Z.
3. Однородные уравнения
В общем случае однородное тригонометрическое уравнение имеет вид:

, где
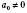
.
Значения
x, при которых
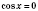
, не является решением уравнения. Действительно, если
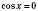
, то уравнение примет вид
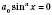
, откуда
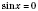
. Но
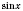
и
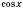
не могут превратиться в 0 одновременно.
Из этого следует, что при делении обеих частей уравнения на
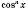
не может произойти потеря корней.
Получаем:
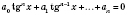
.
Введем новую переменную
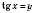
и получим алгебраическое уравнение:
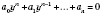
.
Обратите внимание: если
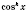
в левой части уравнения можно вынести за скобки, то деление на
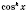
ведет к потере корней.
Примеры
1)
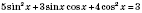
;
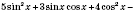
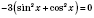
;
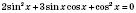
;
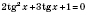
.
Пусть
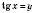
.
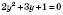
;
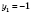
;
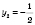
.
а)
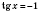
;
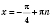
,
n Є
Z;
б)
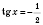
;
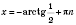
,
n Є
Z.
Ответ:
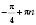
,
n Є
Z;
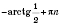
,
n Є
Z.
2)
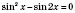
;
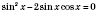
;
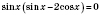
;
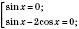
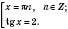
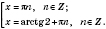 Ответ
Ответ:
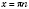
,
n Є
Z,
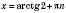
,
n Є
Z.
4. Способ введения вспомогательного аргумента
Этот способ применяется для решения уравнений вида
asin
x ++
bcos
x =
c.
Поделим обе части уравнения на
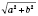
. Получим:
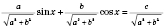
.
Очевидно
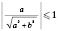
,
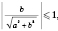
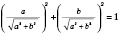
.
Из этого следует, что можно ввести до рассмотрения угол
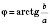
.
Тогда
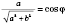
;
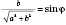
, и уравнение примет вид:
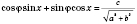
или
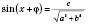
.
Можно принять:
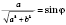
,
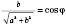
.
Тогда достанем
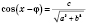
.
Уравнение вида
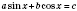
можно решать и другим способом:
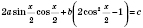
.
Использовав тождество
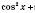
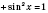
, получим однородное уравнение.
5. Уравнения, содержащие тригонометрические функции в знаменателе. Отбор корней
Эти уравнения сводятся к виду
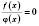
, а затем решают систему
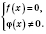 Пример
Пример
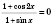
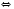
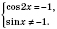
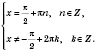
Отбор корней удобно выполнять, воспользовавшись тригонометрическим кругом.
Обозначим на окружности точки, соответствующие углам вида
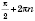
,
n Є
Z.
Затем отбросим (выколи) те из них, которые имеют вид
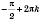
,
k Є
Z (см. рисунок ниже).
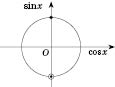 Ответ
Ответ:
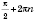
,
n Є
Z.
6. Случай, когда надо найти только определенные развязки
Пример. Сколько решений уравнения
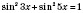
принадлежат промежутку
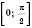
?
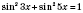
;
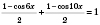
;
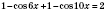
;
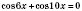
;
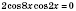
;
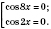
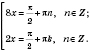
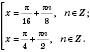
Надо ответить на вопрос, сколько решений принадлежит промежутку
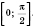 I способ.
I способ. Рассмотрим неравенства:
1)
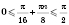
; 2)
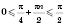
;
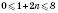
;
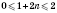
;
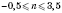
.
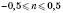
.
n = 0; 1; 2; 3,
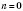
,
поскольку
n Является
Z.
поскольку
n Является
Z.
Таким образом, промежутка
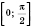
принадлежат пять решений уравнения.
II способ. Можно воспользоваться тригонометрическим кругом, если обозначить на нем соответствующие решениям уравнения точки и отобрать те, что содержатся в первой четверти.