Тригонометрические функции числового аргумента
Рассмотрим единичное (тригонометрическое) круг, центр которого расположен в точке
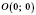
и радиус которого равен 1 (см. рисунок).
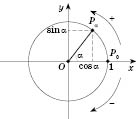
Пусть точка
P0 - это точка (1; 0). Каждую другую точку круга можно достать поворотом
P0 вокруг начала координат. Будем считать отрицательным направление поворота по часовой стрелке, положительным - против.
Точку, которую получим поворотом
P0 вокруг начала координат на угол

, назовем
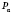
. Очевидно, что значения

могут быть от
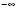
до
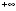
, причем углы, меры которых отличаются на
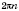
,
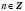
, дают на кругу одну и ту же точку. Например:
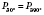
,
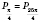
.
Введем обозначения:
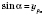
;
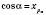
;
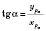
;
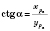
.
Значения
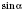
,
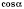
,
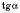
,
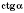
зависит только от угла

.
Для
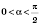
эти определения дают тот же результат, что и определение с помощью элементов прямоугольного треугольника.
Если определение
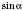
,
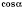
,
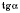
,
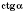
введенные таким образом, то очевидно, что мы получили числовые функции. Действительно, каждому значению
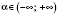
соответствует единственное значение
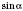
и
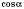
. Также каждому действительному значению
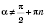 ,
, 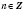
соответствует единственное значение
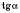
и каждому значению
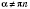 ,
,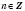
соответствует единственное значение
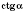
.
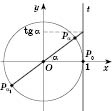
Проведем касательную
t к единичного круга в точке
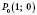
(см. рисунок ниже). Она называется
линией тангенсов, потому что ордината точки пересечения прямой
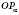
с прямой
t равна тангенсу угла

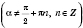
.
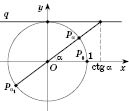
Проведем касательную
q до единичного круга в точке
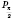
(см. рисунок на с. 73). Для произвольного числа
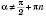 ,
,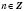
, абсцисса точки пересечения прямой
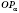
с прямой
q равна котангенсу угла

. Поэтому прямая
q называется
линией котангенсів.
Соотношения между тригонометрическими функциями одного аргумента
1)
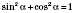
;
2)
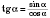
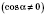
;
3)
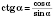
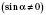
;
4)
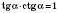
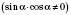
;
5)
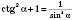
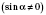
;
6)
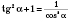
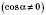
.
Основой для вывода остальных формул являются
формулы сложения:
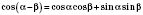
;
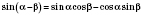
;
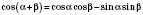
;
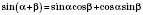
;
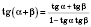
;
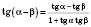
.
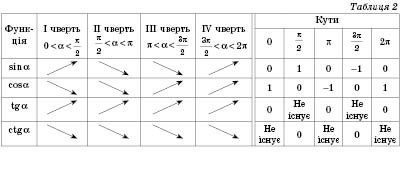
Формулы приведения
Формулы возведения помогают выразить значения тригонометрических функций углов вида
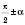
,
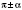
,
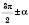
,
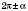
через функции угла

(табл. 1). Соответствующие формулы легко запомнить, пользуясь такими правилами:
1) если аргумент функции имеет вид
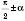
или
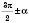
, то название функции меняется на кофункцію (синус на косинус, тангенс на котангенс и наоборот), а если аргумент имеет вид
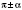
,
, название функции не меняется;
2) перед образованной функцией ставится тот знак, который имеет исходная функция, если

- угол в i четверти.
Используя эти формулы, а также периодичность тригонометрических функций (см. ниже) значение тригонометрической функции произвольного угла свести к значение функции острого угла.
Формулы суммы и разности одноименных тригонометрических функций
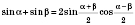
;
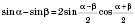
;
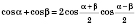
;
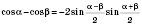
;
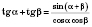
;
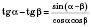
.
Формулы преобразования произведения тригонометрических функций в сумму
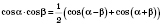
;
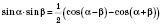
;
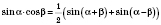
.
Формулы двойного аргумента
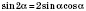
;
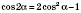
;
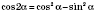
;
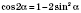
;
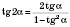
.
Формулы половинного аргумента
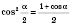
;
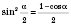
;
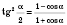
;
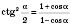
.
Формулы преобразования синуса и косинуса угла через тангенс половины этого угла
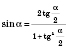
;
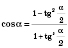
;
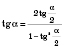
.