Часть 4

ОПТИКА. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ

Раздел 11 ОСНОВЫ ФОТОМЕТРИИ. ОСНОВНЫЕ ЗАКОНЫ ГЕОМЕТРИЧЕСКОЙ ОПТИКИ

11.3. Принцип Ферма

В оптически однородной среде свет распространяется прямолинейно, то есть кратчайшим путем. При прохождении света из одних сред в другие, как мы видели, оно преломляется и отражается на их границах, то есть путь его становится ломаной. В неоднородных средах, где коэффициент преломления n непрерывно изменяется, световые лучи искривляются. Путь, по которому распространяется свет в неоднородном среде, можно определить, руководствуясь принципом, установленным 1662 г. французским математиком П. Ферма.

По принципу Ферма свет распространяется по такому пути, что время, необходимое для его прохождения от одной точки к другой, имеет наименьшее значение.

Если среда имеет показатель преломления n, то скорость света в нем будет υ = с/n, где с - скорость света в вакууме. Следовательно, время, в течение которого свет проходит расстояние l в среде с показателем преломления n, определяется соотношением

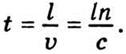
Произведение геометрического пути l на показатель преломления n называют оптическим путем. Пусть свет проходит несколько сред с показателями преломлений n₁,n₂,n₃ (рис. 11.5). Из точки А свет попадает в точку В путем AMNB, для которого время

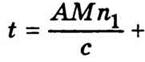
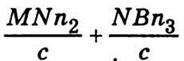
имеет наименьшее значение. Поскольку скорость света с в вакууме является величиной постоянной, то можно сформулировать принцип Ферма так: свет распространяется между точками А и B так, что оптический путь

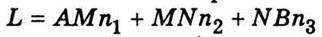
имеет минимальное значение.

Однако для того чтобы принцип Ферма отражал фактическое состояние дел, ему надо дать более общее определение, чем это сделано самим П. Ферма, а именно: свет распространяется по пути, оптическая длина которого экстремальная, то есть либо минимальная, либо максимальная, либо стационарная (одинаковая для всех возможных путей).

Примером стационарного значения оптического пути есть случай отражения лучей от внутренней зеркальной поверхности эллипсоида вращения, в одном из фокусов которого находится точечный источник S (рис. 11.6). Световые лучи, идущие от точечного источника S, после отражения от произвольных точек D₁, D₂, D₃ зеркала, совпадают в втором фокусе эллипсоида S₁. По известной свойством эллипсоида

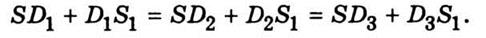
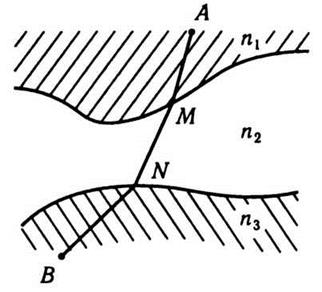
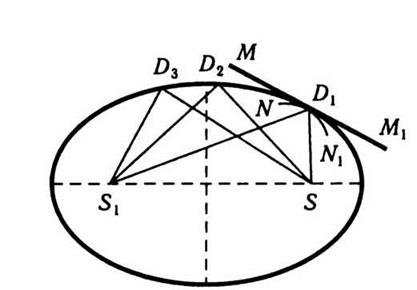
Рис. 11.5 Рис. 11.6

Отражения от поверхности меньшего кривизны, например от плоскости ММ₁ касательной к эллипсоида, соответствует минимуму, а отражения от поверхности NN₁ большей кривизны - максимума длины пути (или времени прохождения).

П. Ферма считал, что его принцип вытекает из еще более общего принципа целенаправленности: «природа всегда придерживается кратчайшего пути». Такое теологическое толкование принципа Ферма было распространено в XVII и XVIII вв. Однако этому толкованию резко противоречат все случаи, соответствующие наибольшему времени. Можно доказать, что принцип Ферма является одним из последствий волновой природы света, но он справедлив только для сферы применения методов геометрической оптики.

Руководствуясь принципом Ферма, можно достать законы геометрической оптики, например законы преломления и отражения света.